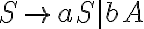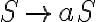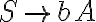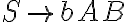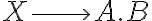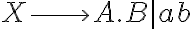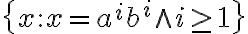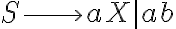[Ejercicio 3][Parte B] Gramaticas Regulares

[Ejercicio 3][Parte B] Gramaticas Regulares

de Juan Martin Nuñez Pena -
Número de respuestas: 4

Buenas.

Tengo una consulta sobre las gramaticas regulares, por que no me termina de quedar claro como son sus reglas.

Tengo entendido que una gramatica regular es una gramatica libre de contexto, con las restricciones de que sus variables siempre aparezcan del mismo lado y que sean de la forma, S->wA o S->w siendo w una variable terminal y en caso de que sea una gramatica lineal derecha.

Si todo lo anterior es correcto, no me termina de quedar claro si es que puede aparecer mas de una variable del lado derecho de las reglas, si estan separados por un pipe, es decir:

S->aS|bA

A->bB|aA|epsilon

B->aB|epsilon

Esto seria una gramatica regular? Lo que importa es que no aparezcan dos variables dentro del mismo caso del pipe? 

Gracias.


En respuesta a Juan Martin Nuñez Pena

Re: [Ejercicio 3][Parte B] Gramaticas Regulares

de Belen Brandino -
hola,
si claro, es una gramática regular. y esto es porque la regla  S \rightarrow aS | bA es equivalente a tener dos reglas por separado:  S \rightarrow aS y   S \rightarrow bA , y estas producciones (y el resto) tienen la forma requerida para una gramática lineal derecha
en el caso de tener dos variables, algo como  S \rightarrow bAB , ya no cumple con la forma requerida, como bien decis
En respuesta a Belen Brandino

Re: [Ejercicio 3][Parte B] Gramaticas Regulares

de Santiago Gongora -

A la buenísima explicación de Belu sobre la forma de las reglas en las gramáticas regulares, agrego 2 piques relacionados a 2 confusiones comunes, por si llega a ayudar a quedar más claro.

1) ¿Por qué no puede haber dos o más variables en la misma regla?

La primer razón de por qué existe la restricción de que haya como mucho 1 variable por regla es porque sino rompería el paralelismo con el autómata finito.
Permitir una regla como X \longrightarrow A.B sería equivalente a tener un autómata que desde el estado X tiene una transición a A, pero que a la vez es "consciente" de lo que pasa en el estado B, estado que computa una parte de la tira que aún no se procesó. Recordemos que la tira en un autómata finito se lee de izquierda a derecha y no se puede volver a leer ninguna secuencia previamente leída, ni tampoco leer algo que viene "más adelante" de lo que se está leyendo ahora.




Pero quizá el ejemplo más claro es que una regla como X \longrightarrow A.B   podría ser parte de una gramática como:
X \longrightarrow A.B | ab
A \longrightarrow a
B \longrightarrow Xb


Si consideramos a X como el símbolo inicial, lo que está generando esa gramática es  \{x: x=a^ib^i \wedge i\geq1 \} , que ya sabemos que es un lenguaje no regular (y por lo tanto no debería poder ser generado por una gramática regular).

2) ¿Por qué las variables tienen que aparecer siempre a la derecha o siempre a la izquierda?

Supongamos que tenemos un conjunto de reglas que hacen aparecer como máximo una variable, pero no respetan que sea siempre del mismo lado, como por ejemplo:
S \longrightarrow aX | ab
X \longrightarrow Sb \

Aunque a simple vista esta gramática parezca regular, en realidad no lo es. El hecho de poder llamar a sus variables desde la izquierda y desde la derecha hace que el lenguaje generado por esta gramática sea, al igual que en el ejemplo anterior, \{x: x=a^ib^i \wedge i\geq1 \} .

Fin

Con la gran explicación de Belu ya re bastaba, pero me quedé manijeado en que capaz a algun@ le sirve tener estos "contraejemplos" para razonar el por qué de las restricciones que tienen las gramáticas regulares.



Bueno listo me voy a jugar a la compu,
Santi