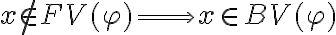Ejercico 8 Parte D

Ejercico 8 Parte D

de Diego Ismael Marichal Chavez -
Número de respuestas: 3

Hola, estoy teniendo una duda en esta parte, segun yo y lo que entiendo de ligaduras, esta afirmacion es falsa, para esto intento armar un contra ejemplo, entiendo que si 

x \notin FV(\varphi) \Longrightarrow x \in BV(\varphi)

Entonces si t es una funcion, esta se puede ligar, pero aqui esta mi duda, ¿se liga la funcion o solo la variable que esta en la funcion? 

Segun entiendo estos conjuntos (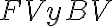FV y BV) tienen variables y no funciones, pero en ese caso no entiendo el ejercicio que se resuleve en el practico (video de youtube), lo unico que puedo vincular es que la eliminación de una variable libre se toma como una nueva ligadura, pero no estoy seguro.

Saludos

Diego

Ejercicio a resolver: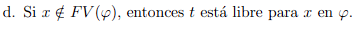 

Ejercicio del practico (video de youtube):
En respuesta a Diego Ismael Marichal Chavez

Re: Ejercico 8 Parte D

de Guillermo Calderon - InCo -

Hola Diego:

En el curso se usan dos versiones de la definición de la relación término libre para una variable en una fórmula.

La definición formal (recursiva sobre FORM) es la que aparece en las diapos de Sintaxis de Primero Orden (pag. 50).

En el video se usa una versión simplificada que es equivalente:

  • Decimos que el termino t no está libre para la variable x en α si el resultado de la sustitución α[t/x] tiene ligaduras nuevas que no estaban en la fórmula α.

  • En caso contrario, si no aparecen nuevas ligaduras, decimos que sí, t está libre para x en α

Esta definición es un poco informal pero la tomamos como válida para nuestro curso.

Con respecto al ejercicio que estás consultando:

  • 8d) Si x no ocurre libre en α, significa que la sustitución no cambia nada, esto es α y α[t/x] son la misma fórmula. Por lo tanto, no aparecen ligaduras nuevas luego de sustituir y entonces: t está libre para x en α.

Si no queda clara, volvé a preguntar.

En respuesta a Guillermo Calderon - InCo

Re: Ejercico 8 Parte D

de Diego Ismael Marichal Chavez -
Me quedo claro, pero el ejercicio dice que x no pertenece a FV(alpha), capaz que se confundio con la parte b
Saludos y muchas gracias
Diego