Buenas
El problema radica en los extremos de integración que estas tomando.
Dado que 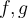 son continuas la región acotada esta delimitada por los puntos de corte de las gráficas.
son continuas la región acotada esta delimitada por los puntos de corte de las gráficas.
Veamos la situación ilustrada en los gráficos de  para entender mejor la situacion y luego resolver el problema. No tienes que saber de antemano como es el grafico, es solo para entender mejor en este caso como estamos trabajando.
para entender mejor la situacion y luego resolver el problema. No tienes que saber de antemano como es el grafico, es solo para entender mejor en este caso como estamos trabajando.
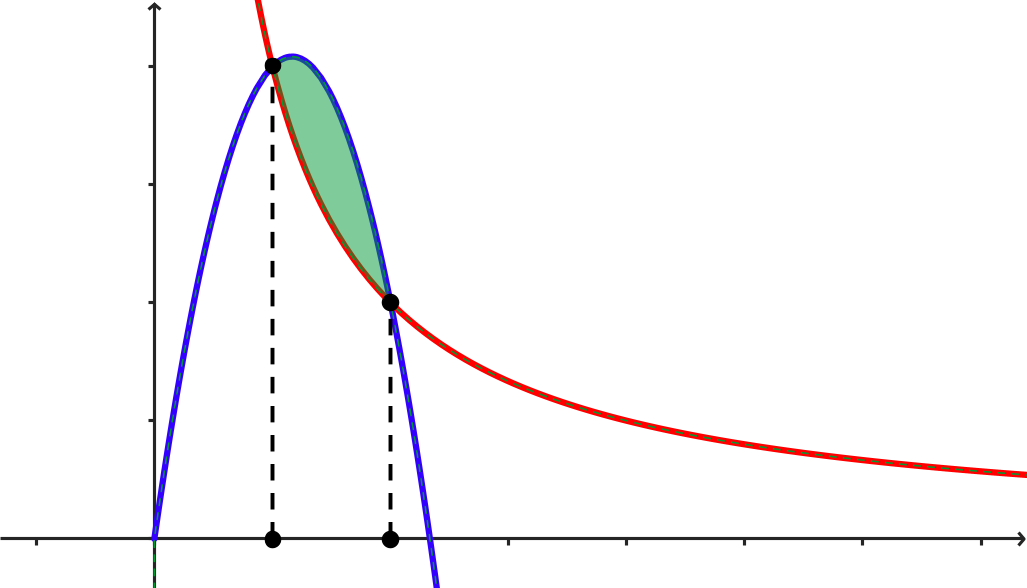
Los puntos de corte son de la forma 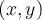 donde
donde  es decir buscamos
es decir buscamos 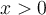 tales que
tales que  . Los puntos podrian ser muchos pero en este caso son 2.
. Los puntos podrian ser muchos pero en este caso son 2.
Esta ecuación es equivalente a 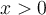 tales que
tales que  .(simplemente multiplique por
.(simplemente multiplique por  )
)
Es decir tienes que encontrar las raices de un polinomio de grado 3 (aunque 1 es una raiz evidente)
Desde aqui puedes encontrar las otras raices que son  pero esta última no cumple
pero esta última no cumple 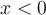
Resumiendo, el polinomo  tiene como raices
tiene como raices  de donde su signo es
de donde su signo es
- negativo para

- positivo para

Como  las funciones
las funciones 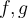 cumplen que:
cumplen que:
Tenemos asi que el area encerrada es 
O lo que es lo mismo 
Tienes otros ejemplos de ejericios similares aqui https://eva.fing.edu.uy/pluginfile.php/473352/mod_resource/content/1/area%20entre%20curvas%202.pdf
Cualquier duda vuelve a escribir
Saludos

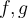


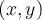

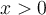




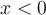





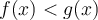
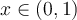
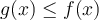
![x \in [1,2] x \in [1,2]](https://eva.fing.edu.uy/filter/tex/pix.php/5e45ec4bc7e60fb589a8593c3007ea20.png)