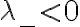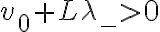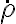Foro: parciales y exámenes

Buenas estaba haciendo el ejercicio 1 de este parcial y me surgieron dos dudas.

(1) parte d) 

A mi me quedo el mismo tiempo que al cual llegan en la solución $t^{*} =\frac{1}{\lambda_{+}-\lambda_{-}} Ln(\frac{v_{0}+L \lambda_{+}}{v_{0}+L \lambda_{-}})$

Ahora cuando quiero ver para que valores de 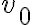$v_{0}$ la partícula llega a $O$  considero que 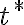$t^{*}$ tiene que ser mayor que cero. Esto ocurre cuando al argumento del logaritmo es mayor a 1. Adjunto foto del razonamiento:

Haciendo esto llego a la misma solución, tengo que considerar que por lo que multiplico es mayor que cero para que no se invierta la desigualdad (si no se cumple e invierto la desigualdad llego a un absurdo, como que $\lambda_{+} < \lambda_{-}$) . Pregunto esto ya que en la solución pide que el argumento del logaritmo se mayor que cero. Esto podría dar lugar a tiempo negativo que no se como interpretar físicamente.

(2) parte e)

Cuando llego a la formula de la normal tengo que 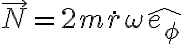$\vec{N}=2m\dot{r}\omega \hat{e_{\phi}}$ que como 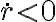$\dot{r} < 0$ en realidad es negativa. Quería preguntar como se interpreta esto. Esto implica que la aceleración según 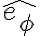$\hat{e_{\phi}}$ es negativa? O tendría que poner un signo para compensar? Intuitivamente tiendo a pensar que la normal es según 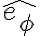$\hat{e_{\phi}}$ por como rota la barra.

En la parte (e) cuando quiero hallar el trabajo de la fuerza reactiva tangencial a la barra, si quiero usar que 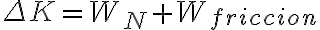$\Delta K = W_{N}+W_{friccion}$ primero calculo el trabajo de la normal que me da positivo, lo cual tiene sentido ya que la Normal es a favor del movimiento. Sin embargo en la solución obtiene un resultado negativo que no comprendo del todo.

Saludos.