Consultas de pruebas anteriores

Buenas

Este ejercicio usa los teoremas de Bolzano y Weierstrass

Veamos primero tu dibujo. En tu dibujo la función llega a valer 0 y llega a valer 5 (y en caso de no hacerlo no seria continua). Sin embargo el ejercicio dice que la función no puede valer 0, ni 5 (el codominio de la función es 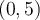$(0,5)$)

La razón por la que no hay funciones sobreyectivas es debido a que las funciones continuas en un intervalo (en este caso $[0,2]$) tiene máximo y mínimo, es decir la imagen de $f$ es $[a,b]$ donde $a = \min(f)$ y $b = \max(f)$.

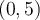Como $\text{Im}(f) \subset (0,5)$ el máximo tiene que ser estrictamente menor a 5, y el mínimo estrictamente mayor que 0, por tanto $[a,b]$ esta estrictamente incluido en el intervalo $(0,5)$, es decir la imagen no es todo el intervalo 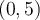$(0,5)$ y no es sobreyectiva.

Respecto a la inyectividad, Aplicando valor medio en $[0,1]$ tienes que existe $c \in [0,1]$ tal que $f(c) = 3 = f(2)$ por tanto no es inyectiva.

Cualquier cosa vuelve a escribir

Saludos