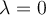Ejercicio 2 parcial 2020

Re: Ejercicio 2 parcial 2020

de Juan Piccini -
Número de respuestas: 0
Hola Melanie.
Una forma de verlo es la siguiente:
Recuerda que si Av=\lambda v, entonces A^nv=\lambda^n v.
Por tanto si Av=\lambda v, entonces O=A^3v=\lambda^3 v.
Como v\neq O, tiene que ser \lambda=0.
Esto ya dice que A tiene solamente un val.p.
Si fuese mg=4, todos los vectores del espacio serían vec.p. en cuyo caso tendríamos A=O y no podría ser A^2\neq O.
Si fuese mg=3, la forma de Jordan sería un bloque 4x4 con 3 subloques cuyos  tamaños deben sumar 4.
Esto nos deja con dos bloques 1x1 y uno 2x2, con lo que J= \left( \begin{matrix} 0 & 0&0&0 \\ 0&0&0&0 &\\0&0&0&0\\0&0&1&0 \end{matrix} \right) .
En ese caso puede verse que J^2=O, con lo que debería ser A^2=P^{-1}J^2P=O, en contra de la letra.
El caso mg=1 puede descartarse razonando en forma similar a lo que hemos venido haciendo.
Espero haber aclarado tu duda.
Saludos
J.