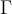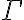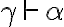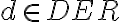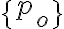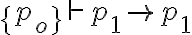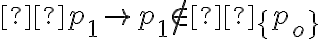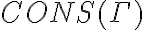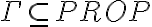Hola, no estoy pudiendo dar ejemplos de teorías cuando me los piden en el práctico. En el video de introducción al práctico menciona que el conjunto {p0} no es teoría, pero no estoy entendiendo porqué no lo es. Acaso puedo derivar algo más que p0 del conjunto {p0}? Agradezco me den algunos de ejemplos de conjuntos que son teorías para entender un poco mejor.
Gracias!
. A este conjunto 
de fórmulas, se le llama Axiomas.
significa que hay una derivación 
tal que 
y (ATENTI!!!! :-) ) 
Esto hace que los teoremas, que cumplen que 
se puedan derivar de cualquier conjunto de fórmulas.
Por lo tanto, para ver que 
no es teoría, hay que probar que hay alguna fórmula que no está en ese conjunto, pero se deriva de él. O sea,
y ver que 
Dicho de otra forma, una teoría, siempre es 
para algún 
.
Espero que quede claro.
Saludos
FDO.