Hola,
Para probar lo que decís tendrías que demostrar que no existe ninguna función tal que su gradiente es exactamente
tal que su gradiente es exactamente 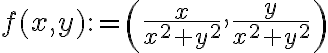 . En otras palabras tendrías que ver que
. En otras palabras tendrías que ver que  no es un campo de gradientes. La forma más barata de ver esto es haciendo lo que hicimos en clase, es decir que en la circunferencia de centro 0 y radio 1 su integral de línea no es 0.
no es un campo de gradientes. La forma más barata de ver esto es haciendo lo que hicimos en clase, es decir que en la circunferencia de centro 0 y radio 1 su integral de línea no es 0.
Para la parte b) fijate que el logaritmo esta definido de forma holomorfa en todos los complejos menos una semirrecta, no en todo el plano compleja menos el 0. Para ver que coinciden localmente tomate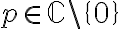 y en un entorno
y en un entorno 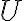 de
de  tomate la función
tomate la función 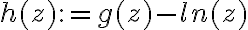 , fijate que la derivada de
, fijate que la derivada de  es 0, por ende
es 0, por ende 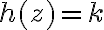 con
con  constante. Con esto casi estarías, quedaría ver alguna cosa más.
constante. Con esto casi estarías, quedaría ver alguna cosa más.
Cualquier cosa si no termina de salir avisame!
Saludos
Para probar lo que decís tendrías que demostrar que no existe ninguna función
 tal que su gradiente es exactamente
tal que su gradiente es exactamente 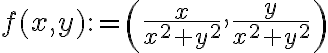 . En otras palabras tendrías que ver que
. En otras palabras tendrías que ver que  no es un campo de gradientes. La forma más barata de ver esto es haciendo lo que hicimos en clase, es decir que en la circunferencia de centro 0 y radio 1 su integral de línea no es 0.
no es un campo de gradientes. La forma más barata de ver esto es haciendo lo que hicimos en clase, es decir que en la circunferencia de centro 0 y radio 1 su integral de línea no es 0.Para la parte b) fijate que el logaritmo esta definido de forma holomorfa en todos los complejos menos una semirrecta, no en todo el plano compleja menos el 0. Para ver que coinciden localmente tomate
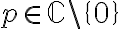 y en un entorno
y en un entorno 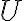 de
de  tomate la función
tomate la función 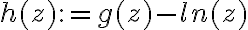 , fijate que la derivada de
, fijate que la derivada de  es 0, por ende
es 0, por ende 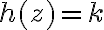 con
con  constante. Con esto casi estarías, quedaría ver alguna cosa más.
constante. Con esto casi estarías, quedaría ver alguna cosa más.Cualquier cosa si no termina de salir avisame!
Saludos
