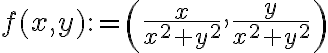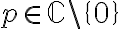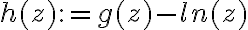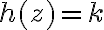Hola, quisiera si me pudieran dar una idea de cómo encarar estas demostraciones, porque no estoy llegando a nada
para la parte a, se me había ocurrido asumir que existe esa g holomorfa, y como es holomorfa entonces g'(z) = ux -iuv y además cumpliría las ecuaciones de C-R. Como ya me dan g'(z) calculé ux, uy, vx, vy usando C-R, pensé que llegaría a una contradicción pero todo da correcto aparentemente, lo único que se me ocurre es argumentar que no existe u tal que uy y ux sean las cosas a las que llegué, mismo con v, entonces podría decir que g no puede ser de la forma g=u+iv y que por ende no es holomorfa ya que no existe dicha g, pero no veo cómo probar eso, llegué a que
ux = x / (x^2 + y^2)
uy= y / (x^2 + y^2)
y luego con C-R que vy=ux y vx=-uy
para la parte b, me parece que g debe ser g(z)=In(z), el logaritmo es holomorfo pero no alrededor del 0, así que creo que no debería haber problema. Si z no tiene parte imaginaria entonces coincide con el log clásico como dice ahí. Creo que hay que relacionar la parte b con la parte a, me parece por un tema de derivación, ya que las funciones holomorfas son derivables y la parte a ya te dice que esa g no es derivable (dejando de lado que no existe), creo que con eso se solucionaría pero no sé si hay que argumentar más
gracias