Consultas de pruebas anteriores

Buenas

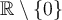La funcion $f$ esta definida en $\mathbb{R} \setminus \{0\}$ es decir no esta definida en 0.

Lo que plantea el ejercicio es si existe una función 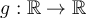$g:\mathbb{R} \to \mathbb{R}$ que sea una extension de la $f$ que sea continua en 0. Veamos que significa ser una extension.

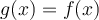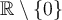La función $g$ es una extensión de $f$ si se cumple $g(x) = f(x)$ para todo $x$ en el dominio de $f$, en este caso $\mathbb{R} \setminus \{0\}$. Es una extension en el sentido que ampliaste el dominio, pero no cambiaste la funcion donde ya estaba definida.

En este ejemplo para que g sea continua en 0, se tiene que cumplir que exista $L \in  \mathbb{R}$ tal que

$\displaystyle \lim_{x \to 0} g(x) = L = \lim_{x \to 0^{+}} g(x) = \lim_{x \to 0^{-}} g(x)$

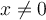Pero como $g(x) =  f(x)$ para todo  $x \neq 0$ se tiene que $\displaystyle \lim_{x \to 0^{+}} g(x) =  \lim_{x \to 0^{+}} f(x) = +\infty$, es decir el limite no puede ser finito y por tanto $g$ no puede ser continua en 0.

Cualquier cosa vuelve a escribir

Saludos