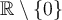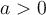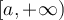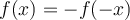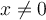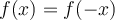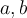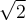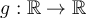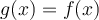Buenas
Vamos parte por parte
Parte 8 del VF:
El bosquejo es eso, un bosquejo, para obtener conclusiones debes tener cuidado. La letra del problema dice que  tiene como dominio
tiene como dominio 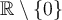 , sin embargo en el grafico que se muestra no queda claro cuanto vale
, sin embargo en el grafico que se muestra no queda claro cuanto vale  pero como
pero como  esta en el dominio
esta en el dominio  tiene que ser algo, lo único que podemos decir es que es mayor que 15, o menor que -15.
tiene que ser algo, lo único que podemos decir es que es mayor que 15, o menor que -15.
Tratemos entonces en esta parte de trabajar con la definición de la función (observa que te dan la expresión algebraica al iniciar el problema).
Dado 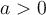 , la función
, la función  es continua en el intervalo
es continua en el intervalo 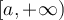 .
.
Para probar que esta acotada en este intervalo hay que usar el teorema de Weierstrass y que  . Estas propiedades aun no las hemos visto en el curso, si ya las conoces y no te das cuanta como aplicarlas vuelve a escribir ahora, sino espera a que las veamos y vuelve a escribir alli
. Estas propiedades aun no las hemos visto en el curso, si ya las conoces y no te das cuanta como aplicarlas vuelve a escribir ahora, sino espera a que las veamos y vuelve a escribir alli
Parte 9 del VF:
Efectivamente se deduce del bosquejo (también de la expresión)
Parte 10 de VF:
Efectivamente la función cumple que 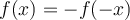 para
para 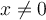 . ¿Puede haber algún valor para el cual se cumple simultaneamente que
. ¿Puede haber algún valor para el cual se cumple simultaneamente que 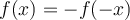 y
y 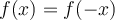 . Para visualizarlo mejor llamemos
. Para visualizarlo mejor llamemos  y
y  ¿existen
¿existen 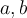 tal que
tal que  ? Intenta entender que pasa con a y b y revisa si la función puede cumplir lo que se pide. Cualquier cosa vuelve a escribir.
? Intenta entender que pasa con a y b y revisa si la función puede cumplir lo que se pide. Cualquier cosa vuelve a escribir.
Ejercicio 1 MO
La descripción de A en la segunda linea esta mal (pues falta intersectar con 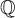 )
)
La notación de la tercera linea no es del todo correcta pero se entiende, una forma similar de escribirlo seria  .
.
Lo que dices relativo a supremo ínfimo máximo mínimo esta bien.
Para verifica que no tiene máximo puedes ver que el supremo es 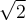 y ese valore no esta en A por lo tanto A no puede ter máximo. Ya que si un conjunto tiene máximo debe coincidir con el supremo.
y ese valore no esta en A por lo tanto A no puede ter máximo. Ya que si un conjunto tiene máximo debe coincidir con el supremo.
Cualquier consulta vuelve a escribir
Saludos