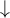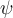Ejercicio 9.a

Ejercicio 9.a

de Anthony Matias Cuña Silveira -
Número de respuestas: 1

Buenas, intentando hacer este ejercicio siguiendo las pautas dadas en la presentación del práctico para la demostración, no logro entender muy bien como hallar un elemento \psi \in \text{PROP}_{\{\downarrow\}} \quad \text{tal que} \quad \alpha' \land \beta' \equiv \psi

En la demostración que se muestra en el video, se explica que la misma se puede obtener viendo la definición de la valuación, sin embargo no logro ver muy bien cómo conseguirla. Agradecería una ayuda sobre como encontrarlo. Gracias.
En respuesta a Anthony Matias Cuña Silveira

Re: Ejercicio 9.a

de Guillermo Calderon - InCo -

Hola:

Para hacer la parte del conectivo \downarrow te recomiendo considerar el conjunto functionalmente completo ${\lor,\neg}$. Creo que queda más fácil, aunque también se puede hacer con $\land$.

Entonces, en el paso inductivo tendrías que hallar:

  • \psi \in \mathrm{PROP}_{{\downarrow}} que sea equivalente a \alpha' \lor \beta'

Para obtener esa expresión \psi tenés que tener en cuenta:

  • que podrías inicialmente pensar esa fórmula \psi usando negación y \downarrow y luego convertir la negación usando la sugerencia.

  • las tablas de verdad de ambos conectivos nos pueden dar una idea de cómo hacerlo: