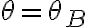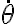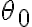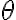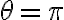Hola, me surgió una nueva duda con este ejemplo. De la descomposición según el versor 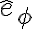 de la segunda ley de newton se obtiene que
de la segunda ley de newton se obtiene que 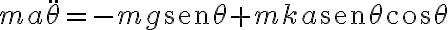 que luego de preintegrar e integrar obtengo que
que luego de preintegrar e integrar obtengo que  Ahora, la pregunta es: ¿cómo se supone que despeje
Ahora, la pregunta es: ¿cómo se supone que despeje 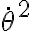 de ahí para sustituir en la ecuación asociada a
de ahí para sustituir en la ecuación asociada a 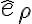 ? Porque yo podría definirme
? Porque yo podría definirme  como constante si dejo
como constante si dejo 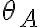 y
y 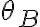 constantes, como función de una variable si dejo alguno de los dos variables (y dependiendo de cuál deje variable me cambiaría el signo) o incluso como función de 2 variables. Ahí es donde me confunde. ¿O vale integrar sin extremos y tomarme simplemente una posible primitiva de
constantes, como función de una variable si dejo alguno de los dos variables (y dependiendo de cuál deje variable me cambiaría el signo) o incluso como función de 2 variables. Ahí es donde me confunde. ¿O vale integrar sin extremos y tomarme simplemente una posible primitiva de 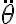 para sustituirla en la ecuación asociada a
para sustituirla en la ecuación asociada a 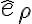 ? En cuyo caso podría evaluar si
? En cuyo caso podría evaluar si  solamente en función de
solamente en función de  sin tener en cuenta
sin tener en cuenta 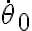 .
.
Este ejemplo me viene generando demasiadas dudas, perdón x)

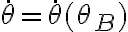
![N\geq 0\:\forall\theta\in[0,\pi] N\geq 0\:\forall\theta\in[0,\pi]](https://eva.fing.edu.uy/filter/tex/pix.php/7b3230926322031ae322c92f8e67e408.gif)