Buenas,
Quería consultar si estaría bien mi cálculo de los 3 algoritmos:
Algoritmo 1:
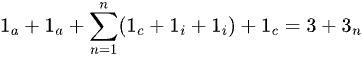
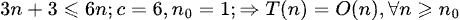
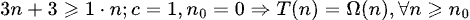
Algoritmo 2:
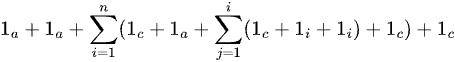
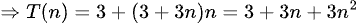
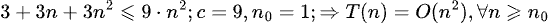
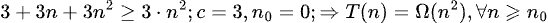
Algoritmo 2:
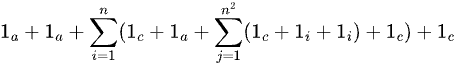
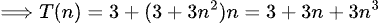
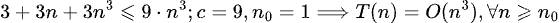
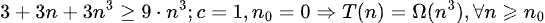
Muchas gracias desde ya!
Mathías
Buenas,
Quería consultar si estaría bien mi cálculo de los 3 algoritmos:
Algoritmo 1:
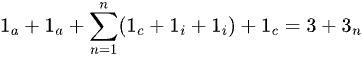
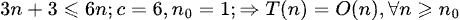
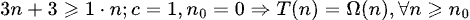
Algoritmo 2:
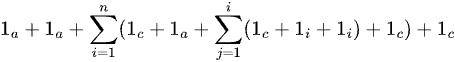
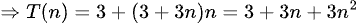
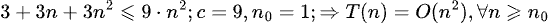
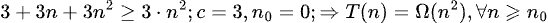
Algoritmo 2:
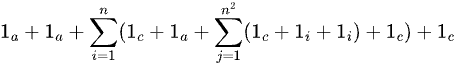
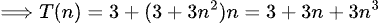
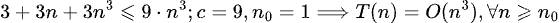
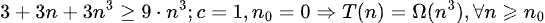
Muchas gracias desde ya!
Mathías
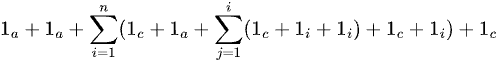
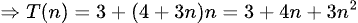
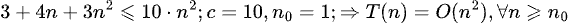
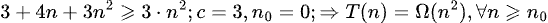
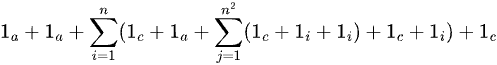
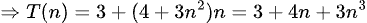
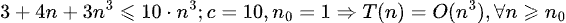
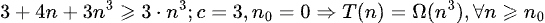
Gracias Profe!