En la expresión que planteas aparecen cosas "parecidas": 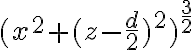 y
y 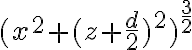 . Para el caso de
. Para el caso de 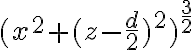 , te recomiendo que empieces por desarrollar
, te recomiendo que empieces por desarrollar 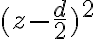 , para luego dividir entre algo conveniente que te deje
, para luego dividir entre algo conveniente que te deje 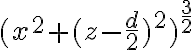 de la forma
de la forma 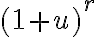 con
con 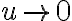 y así poder usar la aproximación. Para esto es importante recordar que para calcular el campo de un dipolo tomamos como hipótesis que
y así poder usar la aproximación. Para esto es importante recordar que para calcular el campo de un dipolo tomamos como hipótesis que 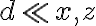 . Lo mismo para
. Lo mismo para 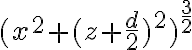 .
.
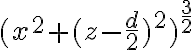 y
y 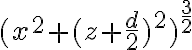 . Para el caso de
. Para el caso de 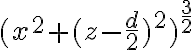 , te recomiendo que empieces por desarrollar
, te recomiendo que empieces por desarrollar 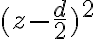 , para luego dividir entre algo conveniente que te deje
, para luego dividir entre algo conveniente que te deje 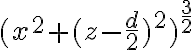 de la forma
de la forma 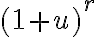 con
con 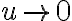 y así poder usar la aproximación. Para esto es importante recordar que para calcular el campo de un dipolo tomamos como hipótesis que
y así poder usar la aproximación. Para esto es importante recordar que para calcular el campo de un dipolo tomamos como hipótesis que 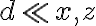 . Lo mismo para
. Lo mismo para 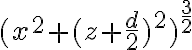 .
.Espero haber sido clara, sino volvé a preguntar.
Saludos,
Juliana
Saludos,
Juliana
