Buenas!, Quisiera saber si la demostración de este ejercicio esta correcta. Me disculpo de antemano por la letra 
Buenas Agustín,
Gracias por compartir tu desarrollo.
Tus razonamientos son correctos. Hay algunos aspectos a mejorar en la comunicación de tu demostración.
En particular, la proposición que quieres demostrar no es que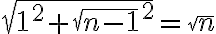
.
Te conviene llamar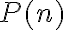
: "es posible construir un segmento de longitud 
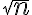con una regla que tiene la longitud unidad marcada y un compás."
Entonces, la proposición que quieres demostrar es que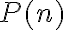 es cierta para todo número natural 
tal que 
.
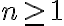Luego, el paso base consiste en probar que es posible construir un segmento de longitud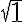
con una regla que tiene la longitud unidad marcada y un compás. Como 
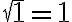, y la regla tiene marcada el segmento de longitud 
, el paso base se cumple.
Hay que reescribir la hipótesis inductiva y la tesis inductiva en tu prueba.
Gracias por compartir tu desarrollo.
Tus razonamientos son correctos. Hay algunos aspectos a mejorar en la comunicación de tu demostración.
En particular, la proposición que quieres demostrar no es que
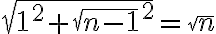. Te conviene llamar
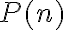: "es posible construir un segmento de longitud 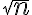con una regla que tiene la longitud unidad marcada y un compás."Entonces, la proposición que quieres demostrar es que
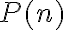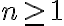es cierta para todo número natural tal que . Luego, el paso base consiste en probar que es posible construir un segmento de longitud
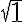con una regla que tiene la longitud unidad marcada y un compás. Como 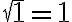, y la regla tiene marcada el segmento de longitud , el paso base se cumple.Hay que reescribir la hipótesis inductiva y la tesis inductiva en tu prueba.
De hecho, la hipótesis inductiva es que 
es cierta para algún número natural 
tal que 
.
es cierta para algún número natural tal que . La tesis inductiva es que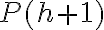 
es cierta.
Durante la demostración del paso inductivo vas a hacer uso del Teorema de Pitágoras.
En resumen: tus razonamientos son correctos. Falta dar forma a la demostración mediante el principio de inducción completa (en particular, declarando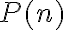 y escribiendo correctamente tanto la hipótesis inductiva como la tesis inductiva).
Cordiales saludos,
Pablo.
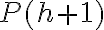es cierta.Durante la demostración del paso inductivo vas a hacer uso del Teorema de Pitágoras.
En resumen: tus razonamientos son correctos. Falta dar forma a la demostración mediante el principio de inducción completa (en particular, declarando
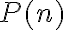y escribiendo correctamente tanto la hipótesis inductiva como la tesis inductiva).Cordiales saludos,
Pablo.
Muchas gracias por responder, se entendió bien!
¡Gracias por avisar, y me alegra que se haya entendido bien!
Hola, cómo estás? Quería saber si mi ejercicio está correcto.
En respuesta a Agustina Arsuaga Maestri
Re: Práctico1 - Ejercicio 8
También tengo la duda de si mi procedimiento es correcto o si tengo cosas a corregir.
Hola Juan Ignacio.
Tenés el mismo problema que Agustina en la definición de la propiedad. Fijate que cuando enunciás el paso inductivo, la hipótesis y tesis inductiva que escribís no tienen nada que ver con lo que definiste arriba como P. Te invito a leer la respuesta que le hice a Agustina y si te queda alguna duda antes de volver a intentar escribir la demosrtación que me preguntes.
Saludos,
Gabriel
Tenés el mismo problema que Agustina en la definición de la propiedad. Fijate que cuando enunciás el paso inductivo, la hipótesis y tesis inductiva que escribís no tienen nada que ver con lo que definiste arriba como P. Te invito a leer la respuesta que le hice a Agustina y si te queda alguna duda antes de volver a intentar escribir la demosrtación que me preguntes.
Saludos,
Gabriel
Hola Agustina.
Tu demostración tiene la estructura correcta para aplicar el principio de inducción completa pero tiene algunos errores graves. Paso a enumerarlos.
Definiste la propiedad como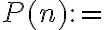
A partir de un segmento de longitud
en el plano es posible construir para cada entero positivo 
un segmento de longitud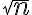 
empleando únicamente regla y compás. El problema con esto es que del lado izquierdo de la definición hay una variable libre 
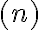y del lado derecho no hay variables libres, puesto que la única variable que aparece (que es la misma) está cuantificada por un cuantificador universal (para todo). Cuando definimos proposiciones abiertas (es decir, con variables libres) estamos definiendo afirmaciones que son paramétricas en algún valor, es decir, para distintos valores de la variable libre producen distintas afirmaciones. Por ejemplo, 
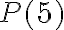debería ser "A partir de un segmento de longitud
en el plano es posible construir un segmento de longitud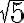 
empleando únicamente regla y compás." Obsérvese cómo estamos haciendo una afirmación sólo sobre el número 
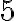y no sobre cada entero positivo .
Tu demostración tiene la estructura correcta para aplicar el principio de inducción completa pero tiene algunos errores graves. Paso a enumerarlos.
Definiste la propiedad como
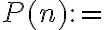A partir de un segmento de longitud
en el plano es posible construir para cada entero positivo un segmento de longitud 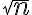empleando únicamente regla y compás. El problema con esto es que del lado izquierdo de la definición hay una variable libre 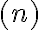y del lado derecho no hay variables libres, puesto que la única variable que aparece (que es la misma) está cuantificada por un cuantificador universal (para todo). Cuando definimos proposiciones abiertas (es decir, con variables libres) estamos definiendo afirmaciones que son paramétricas en algún valor, es decir, para distintos valores de la variable libre producen distintas afirmaciones. Por ejemplo, 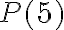debería ser "A partir de un segmento de longitud
en el plano es posible construir un segmento de longitud 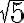empleando únicamente regla y compás." Obsérvese cómo estamos haciendo una afirmación sólo sobre el número 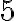y no sobre cada entero positivo .En el enunciado del paso base decís (correctamente) que hay que probar que la propiedad se cumple para 
pero de hecho lo probás para 
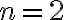(construiste a partir de un segmento de longitud 
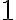un segmento de longitud 
. Bastaba con tomar el mismo segmento con el que comenzás puesto que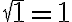 
.
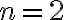pero de hecho lo probás para (construiste a partir de un segmento de longitud 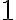un segmento de longitud . Bastaba con tomar el mismo segmento con el que comenzás puesto que 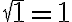.En el enunciado del paso inductivo corresponde aclarar que el natural arbitrario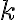 
debe ser mayor o igual a 
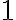(dado que este es el valor para el que se probó el paso base, o al menos se debería haber probado). Si no, 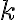podría ser 
.
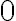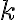debe ser mayor o igual a 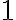(dado que este es el valor para el que se probó el paso base, o al menos se debería haber probado). Si no, 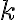podría ser 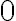.Por último, el objetivo particular de este ejercicio era que vieran que el método de inducción completa sirve para demostrar afirmaciones matemáticas que exceden a lo aritmético. La sustancia de este problema es una construcción geométrica y que esta se puede hacer con regla y compás. Sin embargo en tu desarrollo te limitaste a hacer un par de bosquejos a los que le aplicaste el teorema de Pitágoras sin justificar por qué dichas figuras se pueden trazar con regla y compás. Es central en estas construcciones que con regla y compás se pueden: copiar segmentos de una longitud dada a partir de un punto del plano y una dirección y, trazar segmentos perpendiculares a un segmento dado pasando por uno de sus extremos.
Te invito a que reescribas una vez más tu demostración incorporando estas correcciones y la vuelvas a subir para que la revisemos. Ante cualquier duda que te haya quedado de mi respuesta no dudes en volver a preguntar.
Saludos,
Gabriel