en la solucion del examen proponen usar una curva rectangular que tiene uno de sus lados en el eje real, y por lo tanto corta los polos de la funcion. aplican el teorema de losa residuos contando cada residuo a la mitad.
donde puedo ver un ejemplo mas claro de este metodo ya que no recuerdo haberlo visto en el curso. saludos
Hola, la curva nunca puede pasar por los polos, entonces tenés que hacer un semicirculito pasando por afuera de cada polo.
El problema es que, aunque hagas que el radio de ese semicírculo tienda a cero, la integral sobre ese semicirculo no tiende a cero. Así que hay que restársela a la integral de la curva entera para que esta sea igual a la integral impropia que querés calcular.
Lo que queda entonces es que, si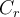 es el círculo de radio r y
es el círculo de radio r y 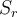 el semicírculo:
el semicírculo:
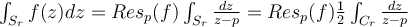
Y ahí se vería porqué decimos que "se toma la mitad" del residuo. Tenés que restarle una mitad por el semicírculo.
Te dejo un rato para que pienses los detalles. Espero que esto te aclare un poco.
El problema es que, aunque hagas que el radio de ese semicírculo tienda a cero, la integral sobre ese semicirculo no tiende a cero. Así que hay que restársela a la integral de la curva entera para que esta sea igual a la integral impropia que querés calcular.
Lo que queda entonces es que, si
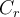 es el círculo de radio r y
es el círculo de radio r y 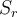 el semicírculo:
el semicírculo: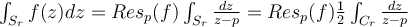
Y ahí se vería porqué decimos que "se toma la mitad" del residuo. Tenés que restarle una mitad por el semicírculo.
Te dejo un rato para que pienses los detalles. Espero que esto te aclare un poco.
Bueno, prosigo con los que les dejé en la clase de consulta.
Los problemas que tuvimos para acotar fue justamente por lo que no tenía en cuenta:
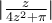
es acotado cuando el módulo de z es muy grande, y parecido a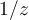 . Entonces, salvo por constantes que sacamos afuera tenemos que si la parte real de
. Entonces, salvo por constantes que sacamos afuera tenemos que si la parte real de  es suficientemente grande
es suficientemente grande
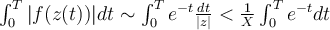
y haciendo crecer X a infinito, se tiene que la integral de este lado tiende a cero. Y es la misma cuenta para el otro lado.
Los problemas que tuvimos para acotar fue justamente por lo que no tenía en cuenta:
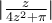
es acotado cuando el módulo de z es muy grande, y parecido a
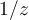 . Entonces, salvo por constantes que sacamos afuera tenemos que si la parte real de
. Entonces, salvo por constantes que sacamos afuera tenemos que si la parte real de  es suficientemente grande
es suficientemente grande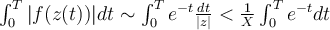
y haciendo crecer X a infinito, se tiene que la integral de este lado tiende a cero. Y es la misma cuenta para el otro lado.
es correcto tomarme una semicircunferencia en vez de una curva rectangular?
por el lema de deformacion de caminos la integral en el arco de la circunferencia con R tendiendo a infinito es 0
Si la integral queda dentro de las hipotesis del lema de deformación, sí. Si no habría que probarlo, no son condiciones suficientes.
En este caso creo que sí, porque el denominador es de segundo orden, pero no he hecho la cuenta.
En este caso creo que sí, porque el denominador es de segundo orden, pero no he hecho la cuenta.
en este caso el limite zf(z) no te da 0, entonces no podes usar el lema.. por eso hay q complicarse con el rectangulo