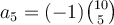hola yo me tranque tambien en este ejercicio tratando de hacer la derivada entonces puse en el wolfram alpha cuanto daba el residuo de (z^2-1)^10/z^11 y da -252 y luego multiplicando por -2pi/2^10 llego al resultado de 63/128pi que es diferente al obtenido en la solucion
otra forma de llegar al mismo resultado es aplicando el teorema de cauchy global para las derivadas donde la derivada decima de (z^2-1)^10 evaluada en z=0 es -10!*2^2*63 que luego multiplicando por -2pi/(10!*2^10) llego de nuevo a que la integral es 63/128 pi
el wolfram alpha te permite hacer la integral de (sen x)^10dx entre 0 y 2pi que es efectivamente 63/128pi
no se me ocurre como hacer los calculos a mano
saludos
dejo los links al wolfram para verificar
residuo:
http://www.wolframalpha.com/input/?i=residue+of+%28z%5E2+-+1%29%5E10%2Fz%5E11
derivada decima:
http://www.wolframalpha.com/input/?i=tenth+derivative+of+%28z%5E2-1%29%5E10+at+z%3D0
integral del seno a la 10 entre 0 y 2pi:
http://www.wolframalpha.com/input/?i=integrate+of+%28sin+x%29%5E10+from+x%3D+0+to+2pi
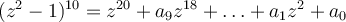
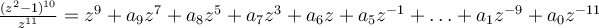
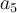 . Este término está dado por ser el quinto término de la potencia décima de un binomio, entonces
. Este término está dado por ser el quinto término de la potencia décima de un binomio, entonces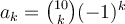 en particular
en particular