Hola, en la tercera afirmacion que dice Si {Ai}i∈I es una familia cualquiera de conjuntos cerrados entonces ∪i∈IAi es un conjunto cerrado. no me queda claro porque es asi. Sé que la union de la familia de conjuntos abiertos es abierto y pense que sería lo mismo con conjuntos cerrados.
Hola. La afirmación "Si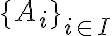 
es una familia cualquiera de conjuntos cerrados entonces 
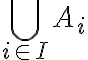es un conjunto cerrado" es falsa. Un contraejemplo es si tomamos, en 
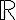, a los 
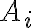como ![A_i = \left[ \frac{1}{i},1 \right]](https://eva.fing.edu.uy/filter/tex/pix.php/1ef5f202866dc07191ded5586a72a938.png "A_i = \left[ \frac{1}{i},1 \right]")
para todo 
. Entonces la unión de todos lo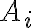s es ![\bigcup_{i \in \mathbb{N}}A_i = (0,1]](https://eva.fing.edu.uy/filter/tex/pix.php/3fc3d1ee7af3081c3962a73da55f3dc4.png "\bigcup_{i \in \mathbb{N}}A_i = (0,1]")
, que no es cerrado.
Como bien decís, la misma afirmación pero para conjuntos abiertos es cierta.
Saludos
Muchas gracias!