Reducciones en tiempo polinomial

Reducciones en tiempo polinomial

de Thiago Caetano Acuña Vinoles -
Número de respuestas: 2

Buenas! Haciendo el ejercicio 3 del Examen de Julio de 2022, al momento de probar que  Independent\ \ Set\leq _P Cocinero , luego de definir la transformación de la forma evidente, quiero probar que efectivamente Independent Set se reduce a Cocinero.

Tengo entendido que esto se puede probar demostrando lo siguiente:
s_X \text{ es una instancia "SI" del problema X} \Leftrightarrow s_Y \text{ es una instancia "SI" del problema Y} siendo s_Y el transformado de s_X.

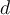Sin embargo, a la hora de probar \big( \Leftarrow \big) , me topé con que el problema de Independent Set no puede modelar la posibilidad de tener algunas aristas dentro del conjunto independiente, cosa que sí hace (de forma análoga con los ingredientes y el parámetro d) Cocinero.

¿Esto quiere decir que Cocinero es estrictamente más dificil que Independent Set? O sea, que no se cumple Cocinero \leq _P Independent\ \ Set

¿Una fórma válida de probar  Independent\ \ Set\leq _P Cocinero sería probar Si\ s_X \text{ es una instancia "SI" del problema X} \Rightarrow s_Y \text{ es una instancia "SI" del problema Y} y Si\ s_X \text{ es una instancia "NO" del problema X} \Rightarrow s_Y \text{ es una instancia "NO" del problema Y}
En respuesta a Thiago Caetano Acuña Vinoles

Re: Reducciones en tiempo polinomial

de Jonathan Murana -
Thaigo como estás?

no se si entendí bien lo que planteas, pero te respondo lo que entendí a ver si ayuda.

la reducción polinomial dice que si tengo una caja negra que resuelve COCINERO entonces puedo resolver INDSET

entonces lo que hacemos es tomar una instancia arbitraria de INDSET y llevarla a una instancia de COCINERO,
resolver esa instancia y luego volver a la solución en INDSET. El tema es que las instancia generadas de
COCINERO podrían tener todas cierta particularidad en la estructura (podrían ser todas de un subprobelma COCINERO). En realidad no nos importa porque la caja negra las resuelve (aunque la estemos "sub-usando" digamos).

Entonces el ⇔ que tenes que probar es:
 dada una instancia arbitraria de INDSET es SI ⇔ la instancia correspondiente de COCINERO es SI.

que no es lo mismo que reducir el problema COCINERO a INDSET.

la forma valida que planteas es correcta lógicamente equivalente al ⇔
no se si en estos casos facilita la prueba

en resumen, creo que tu problema es que estas intentando probar ⇐ con instancias de COCINERO que nunca se generarían con la reducción

saludos