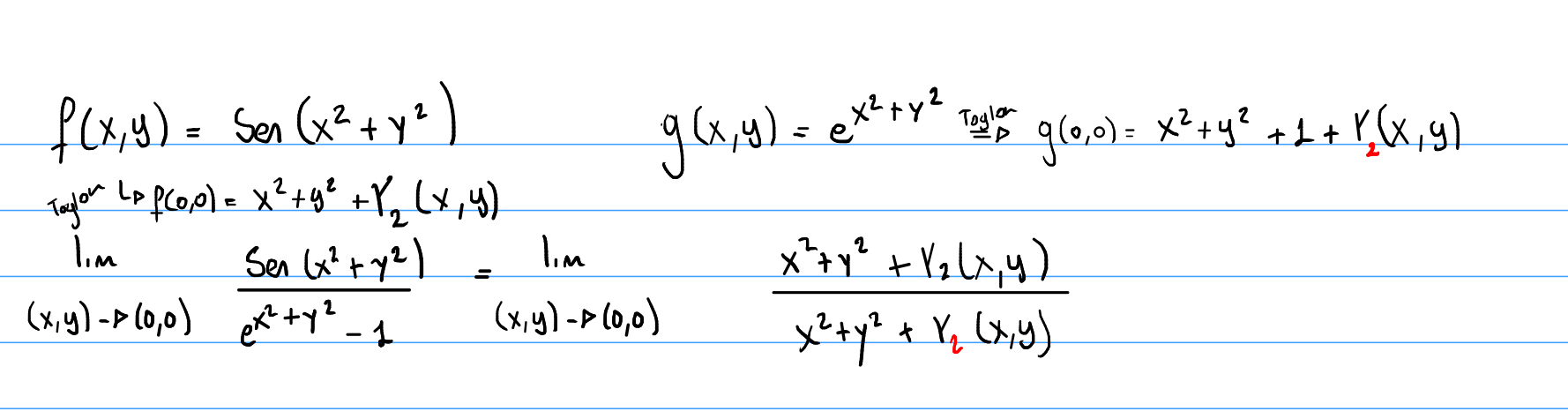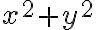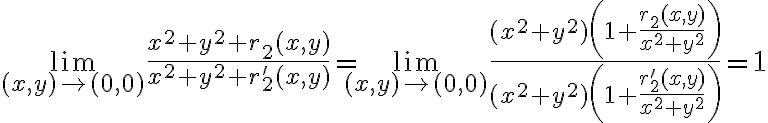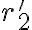Hola tengo una duda con como resolver un limite con Taylor
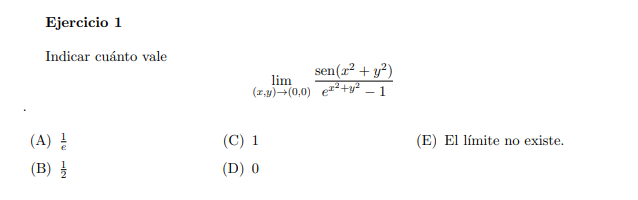
Entiendo que usando equivalentes es inmediato, pero desarrollando con Taylor no me queda claro como eliminar los restos, como son de grado dos ambos tienden a 0 cuando son divididos por x² + y², pero no puedo llegar a eso, alguna sugerencia?