Hola, me podrian explicar por que la respuesta correcta es la D? Yo pense que era la A, porque recorres 98 aristas con dos posibilidades cada una, y en el paso 99 tenes un solo movimiento posible.

Hola, me podrian explicar por que la respuesta correcta es la D? Yo pense que era la A, porque recorres 98 aristas con dos posibilidades cada una, y en el paso 99 tenes un solo movimiento posible.

 y
y  respectivamente.
respectivamente.  caminos cualesquiera de longitud
caminos cualesquiera de longitud  que inician en
que inician en  . Pero hay muchos de ellos que, luego del paso
. Pero hay muchos de ellos que, luego del paso  , ya están en el vértice
, ya están en el vértice  y por lo tanto no van a poder terminar en el vértice
y por lo tanto no van a poder terminar en el vértice  tras agregar un paso. Es por eso que no funciona tu conteo (ese "paso" que agregas a cada uno de los
tras agregar un paso. Es por eso que no funciona tu conteo (ese "paso" que agregas a cada uno de los  caminos no es siempre posible, y esto te lleva a contar en exceso).
caminos no es siempre posible, y esto te lleva a contar en exceso).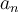 ,
, 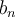 y
y 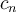 a la cantidad de caminos que inician en el vértice
a la cantidad de caminos que inician en el vértice  , tienen longitud
, tienen longitud  y terminan respectivamente en los vértices
y terminan respectivamente en los vértices  ,
,  , o
, o 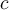 entonces como todos los caminos de longitud
entonces como todos los caminos de longitud  que empiezan en
que empiezan en  son
son 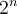 , la regla de la suma nos dice que
, la regla de la suma nos dice que  .
.  . Reemplazando en la primera igualdad tenemos que
. Reemplazando en la primera igualdad tenemos que  .
. 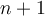 que termina en
que termina en  viene de
viene de  o bien de
o bien de 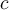 , por lo que
, por lo que  , y como
, y como  tenemos que
tenemos que  . Reemplazando nuevamente tenemos que
. Reemplazando nuevamente tenemos que  , y cancelando un factor común
, y cancelando un factor común 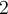 obtenemos que
obtenemos que  con dato inicial
con dato inicial  .
.  y al buscar una particular de la forma
y al buscar una particular de la forma  encontramos
encontramos  . Luego
. Luego  y como
y como  resulta que
resulta que  . Esto significa que
. Esto significa que  y que
y que  . De esta manera obtenemos la respuesta
. De esta manera obtenemos la respuesta 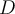 .
. 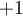 si nos movemos en un sentido o
si nos movemos en un sentido o 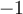 si nos movemos en sentido contrario. Hay que contar las palabras de largo cuya suma es de la forma
si nos movemos en sentido contrario. Hay que contar las palabras de largo cuya suma es de la forma  para algún entero
para algún entero 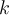 . Es un modo alternativo.
. Es un modo alternativo. 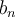 crece como
crece como  . El largo impar "favorece" a terminar en
. El largo impar "favorece" a terminar en  y el par "desfavorece"; de ahí que tenemos los
y el par "desfavorece"; de ahí que tenemos los  y
y  sumando y restando en la solución de la recurrencia. Esto es un enfoque "intuitivo" hacia la solución.
sumando y restando en la solución de la recurrencia. Esto es un enfoque "intuitivo" hacia la solución.