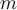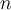Buenas noches,
Realicé un análisis de este ejercicio pero no sé si está bien:
Para que el grafo quede dividido en dos componentes conexas, puedo quedarme con dos subgrafos que tengan n/2 (en el caso par) vértices cada uno. (Si n impar serían dos subgrafos, uno de parte entera(n/2) y otro de parte entera(n/2)+1) tal que si sumo los vértices vuelve a quedar n. Además cada subgrafo tendría la misma cantidad de vértices que aristas (por construcción), o sea que la cantidad de aristas sería n.
La cantidad total de aristas de Kn = n(n-1)/2 (demostrado en el teórico)
Entonces la cantidad de aristas mínimas a eliminar sería el total menos las que dejo para que Kn se desconecte en dos componentes conexas: n(n-1)/2 - n = n(n-3)/2
Agradezco vuestros comentarios.
Saludos!
Alondra.-