Prog3: Práctico 9 - Ejercicio 2

Buenas!

He estado pensando alguna solución para este ejercicio pero la verdad que lo que he pensado no me termina de cerrar, lo comparto por acá:

Supongo seguir una estrategia de d-disparos teniendo los pares:

$\left( c_{1},v_{1}\right) ,\ldots ,\left( c_{m},v_{m}\right) ,1\leq m\leq d$

Basándome la sugerencia pensé estos casos:

Si vendo las acciones del último disparo el día $i$ :
$OPT\left( i,m\right) =OPT\left( i+1,m-1\right) +1000\cdot ( p( v_{i})-p( c_{i}))$ .
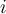Si no vendo las acciones del último disparo el día $i$
$OPT(i,m)=OPT(i+1,m)$

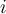
En cuanto a los casos base:
Si estoy en el último día, siempre me va a convenir vender la última acción porque aunque llegue a tener ganancia negativa es mejor que no vender
$OPT(n,m) = 1000 \cdot (p(v_m) - p(c_m)), \forall m:0\leq m \leq k$
Además si no tengo acciones para vender la ganancia es 0, sin importar del día en el que me encuentre.
$OPT(i,0) = 0, \forall i:1\leq i \leq n$

Haciendo el máximo de (1) y (2) y teniendo como caso base (3) y (4), es lo que me parece que podría llegar a ser la solución.

Principalmente, me gustaría saber si por lo menos voy encaminado y en cualquier caso, por dónde podría seguir indagando para llegar a la solución final. Siento que me faltan ver posibles días, pero capaz tengo que confiar en que los veo al armar todos los posibles casos.

Si alguna o algún compa pensó algo también es más que bienvenido :)

Muchas gracias de antemano.

Saludos,

Re: Práctico 9 - Ejercicio 2

de Bruno Emanuel Gandos Telis - domingo, 30 de octubre de 2022, 23:11

Hola, aprovecho esta pregunta también para consultar unas dudas de la letra y mostrar la solución que se me ocurrió.
Lo primero que hice fue definir OPT(i,d) siguiendo la sugerencia como la mayor ganancia mediante una estrategia de d disparos desde los días 1 hasta i.
En la letra del ejercicio se nos aclara que

$0 \leq i \leq n$ y

$0 \leq d \leq k$

Con esta información se me ocurrió la siguiente recurrencia:

OPT(0,d) = 0

$\forall d \in$ {0, .. , k}

OPT(i,0) = 0

$\forall d \in$ {0, .. , n}

OPT(i,d) =

$max$ {1000(

$p(v_d) - p(c_d)$ + OPT(i-1,d-1) , OPT(i-1,d)}

Ahora las preguntas:

¿Tiene sentido que i vaya desde 0 hasta n? En cuyo caso, OPT(0,d) me estaría diciendo que la mayor ganancia con d disparos desde los días 1 a 0 es cero? Tiene sentido esto último?
¿Tiene sentido que d vaya desde 0 hasta k? En cuyo caso, OPT(i,0) me estaría diciendo que hubo una estrategia de 0 disparos desde los días 1 hasta i?

Gracias.

Re: Práctico 9 - Ejercicio 2

de Fernando Fernandez - lunes, 31 de octubre de 2022, 20:21

Hola.
Va bien encaminado pero faltan algunos detalles.
La idea es que OPT(i,d) es la máxima ganancia que se puede obtener desde el día 1 hasta el día i haciendo a lo sumo d disparos (compra-ventas). Nos preguntamos que información de la solución nos sería útil para entender la estructura de los subproblemas. Esa información podría ser si la solución incluye o no una venta en el día i.

Si no incluye una venta en el día i entonces la ganancia máxima se obtiene desde el día 1 hasta el día i-1 con hasta d disparos. De ahí el término que incluiste, OPT(i-1, d).

Pero si se incluye una venta en el día i sabemos que tuvo que haber una compra en algún día previo, digamos c, anterior a i. Se debe sumar p(i) y restar p(c), ya que c e i son los días en que se hace la compra-venta (los valores v_d y c_d que incluís no son conocidos, sino que es lo que se debe determinar, e incluso no se sabe si conviene hacer d compra-ventas o menos). A lo que se obtiene por esa compra-venta hay que sumarle la máxima ganancia que se puede obtener con hasta d -1 compra-ventas (porque una es la que corresponde a los días c e i) pero en los días estrictamente anteriores a c. Es parecido a lo que escribiste pero tenés que tener en cuenta esto último, porque los intervalos que definen cada compra-venta no se pueden solapar.
Todavía nos queda tener en cuenta una segunda información que fue mencionada, y es qué día se hace la compra que corresponde a la venta del día i, o sea cuál es el valor de c. La relación de recurrencia debe considerar cada uno de los posibles valores.

Con respecto a los casos base, d igual a 0 tiene sentido incluso conceptual porque la mejor opción podría ser no hacer ninguna compra-venta. Esto sería lo mejor si los p(i) fueran estrictamente decrecientes.

Con respecto a i = 0, aunque desde un punto de vista de la realidad no tenga sentido puede ser útil para hacer menos complicada la parte genérica de la recurrencia.

Saludos,

Re: Práctico 9 - Ejercicio 2

de Fernando Fernandez - lunes, 31 de octubre de 2022, 20:35

Hola.
Creo que algo de la respuesta a Bruno también se aplica acá.

Tenés que tener en cuenta que no tenemos los pares

$(c1,v1), \dots, (c_d,v_d)$ . Si los tuviéramos no haría falta la recurrencia, se podría calcular la ganancia directamente.

Por la forma en que escribís la recurrencia, OPT(i,m) representa la ganancia máxima que se puede obtener desde el día i hasta el día n haciendo a lo sumo m compra-ventas. Entonces en el día i lo que podés hacer es una compra, no una venta.
¿O es otra la idea que tenés de lo que representa OPT(i,m)?

Saludos,