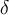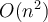Ejercicio 11 del capítulo de Greedy, sección de ejercicios

Ejercicio 11 del capítulo de Greedy, sección de ejercicios

de Ian Ignacy Arazny Casanovas -
Número de respuestas: 2

Hola buenas tardes, estábamos repasando con un compañero este ejercicio y no entendemos esta solución proporcionada, concretamente el motivo por el que divide la mínima diferencia entre dos costos ( 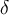\delta ) entre n^{3} , luego de forzar que todas las aristas sean distintas entendemos cómo proceder con el problema. 

El problema es el siguiente,


La solución proporcionada: 


Cualquier tipo de ayuda se agradece,

Saludos,

Ian.
En respuesta a Ian Ignacy Arazny Casanovas

Re: Ejercicio 11 del capítulo de Greedy, sección de ejercicios

de Fernando Fernandez -
Hola.
Esta es mi opinión de por qué el resultado es correcto.

El cambio en los pesos debe lograr
  • cada par de aristas que tuvieran el mismo peso deben pasar a tener pesos diferentes, con el requerimiento adicional de que si una pertenece a T y la otra no, es la que pertenece a T la que queda con peso menor. Esto se logra porque el término que se sustrae incluye a i como factor, que es mayor en las aristas de T; 
  • entre cada par de aristas que tuvieran peso diferente se debe conservar el orden. Es decir que la que tenía menor costo debe seguir teniendo menor costo. Como a cada arista se le resta un valor diferente (por la presencia del factor i) podría ocurrir que a una arista de mayor costo se le reste un valor más grande y quede con menor costo que la otra. Si lo que se resta es menor que \delta esto último no puede ocurrir. El máximo valor que se puede restar es el que corresponde al mayor i, que es igual a la cantidad de aristas, que podría ser de orden O(n^2). Al dividir por n^3 se asegura que todos los términos que se sustraen sean menores a \delta. 
No sé si esto explica la duda.

Saludos,