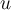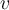Prog3: Simulacro 2018

Buenas tardes, tengo la siguiente duda con el ejercicio 1 de este Parcial Simulacro:

En la parte a), es necesario devolver dicho ciclo de largo mínimo en caso de que exista? De ser así, me gustaría saber si podrían darme una pista o alguna idea con esta parte.

Logré ver y poder devolver el largo del ciclo que sea mínimo, pero no logro ver como poder devolver este ciclo.

Saludos y muchas gracias.

Re: Simulacro 2018

de Federico Gutierrez Scampini - domingo, 9 de octubre de 2022, 17:24

Re tarde, pero me parece que funciona si guardás el nodo por el cual agregaste cada nodo a S en un arreglo parent y luego si llegas a un nodo ya explorado u, tomás el nodo v por el que llegaste a ese nodo ya explorado y seguís por parent hacia atrás hasta encontrarte con ese nodo u, luego completas el ciclo con la arista (v,u). El largo lo obtenes tomando el largo de ese camino hacia atrás + 1 por la arista (v,u), si este largo es menor que el que ya tenías, guardás el ciclo, sino lo descartás, luego seguís con BFS. De este modo ejecutas BFS de un nodo solo, luego las ejecuciones totales del for son 2m que es la suma de los grados de los nodos, y guardar un ciclo lleva a lo sumo n pasos(un ciclo puede ser a lo sumo de largo n), por cada ejecución del for. Por lo que en total tenés T(2m*n), osea O(nm).
Igualmente no se si esta correcto este algoritmo, pero es lo que se me ocurrió.

Re: Simulacro 2018

de Tatiana Rischewski Santomauro - martes, 11 de octubre de 2022, 09:57

Hola Federico,

En BFS no se cumple necesariamente que si llegás a partir de un nodo $x$ a un nodo $u$ ya explorado, recorriendo por parent desde $u$ se llegue nuevamente al nodo $x$ . Esto se cumple para DFS (3.7), pero no para BFS.

En el caso de BFS se sabe que ambos nodos tienen un ancestro en común, y se puede saber en qué capa están cada uno de los nodos (distancia al nodo inicial desde el cual llamé a BFS). Con esto se puede recorrer hacia atrás, usando el arreglo parent, a la vez los ancestros de ambos nodos $u$ y $x$ , hasta llegar a el primer ancestro en común.

De todas formas, si se ejecutara DFS en vez de BFS igual no alcanza con ejecutarlo desde un solo nodo, ya que puede ocurrir que no se recorran todos los ciclos cuando se parte de un nodo solo (encuentra solo los ciclos en los que solamente una de las aristas del ciclo no pertenece al árbol DFS).

Saludos,
Tatiana

Re: Simulacro 2018

de Tatiana Rischewski Santomauro - martes, 11 de octubre de 2022, 09:52

Hola Paula,

Cómo se hace para devolver el ciclo de largo mínimo depende de cómo sea tu algoritmo para encontrar los ciclos. Si se sigue la sugerencia y se aplica BFS desde cada nodo, el problema consiste en devolver el ciclo que se encuentra con BFS.

Se encuentra un ciclo cuando se recorre un nodo que ya se había descubierto (hay una arista $(u, v)$ entre dos nodos ya descubiertos). El ciclo se puede devolver recorriendo el árbol desde los nodos $u$ y $v$ hasta encontrar el ancestro más cercano. Para esto, si ambos nodos están en el mismo nivel, alcanza con iterar a la vez recorriendo el padre de cada uno hasta llegar al mismo nodo, agregando los nodos que se van recorriendo al inicio y al final de un camino. Si no están en el mismo nivel, uno está en un nivel inmediato inferior, por lo que alcanza con moverme primero al padre, que sí está en el mismo nivel, antes de empezar a iterar.

Saludos,
Tatiana