Consultas 2022

Hola,

No entiendo como la forma en la que ordenás las variables es diferente a la de la solución. En la solución se ordenan las variables de manera creciente según el número de la primera instrucción de sus bloques, es decir en el orden en el que aparecen por primera vez.

El if de la linea 14 no es necesario en el algoritmo, pero simplifica la demostración de terminación. En la parte (b) se prueba que nunca se cumple la condición del if al probar que nunca queda ninguna variable sin asignar.

Es correcto que para demostrar la corrección del algoritmo hay que probar que resuelve el problema utilizando la mínima cantidad de celdas de memoria disponible. En este caso, en la solución de la parte (a) se explica que la cantidad mínima de celdas 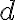$d$ requeridas necesariamente debe cumplir que 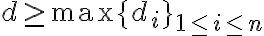$d \geq \smash{\displaystyle\max \{d_i\}_{1 \leq i \leq n}}$. Como el algoritmo planteado utiliza exactamente 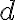$d$ celdas (el mínimo posible), entonces la solución retornada es óptima.

La técnica usada en la demostración es igual a la que se aplica en el libro en la parte “A Related Problem: Scheduling All Intervals” de la sección 4.1. Es posible escribir la demostración usando explícitamente un argumento de stay ahead. Para eso habría que modificar levemente el algoritmo para que solo se use una nueva celda si todas las anteriores están ocupadas. Luego en la demostración de corrección hay que probar que la cantidad de celdas que usa mi solución para asignar las primeras 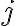$j$ variables no es mayor que la cantidad que usa una solución óptima para asignar las mismas variables. Como en particular se cumple para 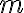$m$, la asignación de mi algoritmo es óptima.

Saludos,
Tatiana