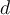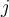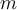Hola! estaba tratando de hacer este ejercicio, y el desarrollo del algoritmo me quedó un tanto diferente
Para empezar no termino de entender porqué ordena las variables en el orden descrito en la linea 2 del algoritmo planteado como solución, en mi caso simplemente pedí que se ordenaran las variables en orden de la primera aparición, pues si los bloques tienen sus lineas consecutivas, me basta saber que variables tengo "detrás" si me detengo en la variable i, sabiendo que todos los bloques de las anteriores variables comienzan antes que el de la variable i.
Luego en la linea 14 toma la decisión de dejar la variable vi sin asignar si el conjunto C es vacío, esto me parece innecesario pues se sabe según la letra que la cantidad de celdas disponibles es suficiente para crear una asignación, por lo que siempre quedaría un espacio de memoria libre para asignarle a vi.
Relacionado con esto último es la ultima duda también, pues en la demostración de corrección pretende probar éste ultimo punto y también que dadas dos variables vi y vj que se solapan en sus bloques, entonces tienen asignadas celdas de memoria diferentes. Tiene sentido esto cuando estamos hablando de un Greedy Algorithm? no deberíamos centrarnos en probar que el algoritmo resuelve el problema utilizando la mínima cantidad de celdas de memoria disponible, utilizando algún argumento de tipo stay ahead o exchange?
Si pudiéramos hacerlo de esta forma, como lo harían?
Gracias y saludos!