Buenas tardes, planteé el ejercicio de esta forma, pero no logro identificar ω en la ecuación que me quedó. Muchas gracias por la ayuda.

Buenas tardes, planteé el ejercicio de esta forma, pero no logro identificar ω en la ecuación que me quedó. Muchas gracias por la ayuda.

 es positiva hacia arriba. ¿Cuál es el origen de coordenadas? Esto es importante, porque el origen de coordenadas no puede estar ubicado en la base del corcho, dado que ese sistema de referencia no es inercial (la base del corcho tiene aceleración no nula, puesto que el corcho describe un movimiento armónico simple).
es positiva hacia arriba. ¿Cuál es el origen de coordenadas? Esto es importante, porque el origen de coordenadas no puede estar ubicado en la base del corcho, dado que ese sistema de referencia no es inercial (la base del corcho tiene aceleración no nula, puesto que el corcho describe un movimiento armónico simple). 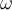 alcanza con que halles la ecuación del movimiento del corcho. Deberías llegar a algo del tipo
alcanza con que halles la ecuación del movimiento del corcho. Deberías llegar a algo del tipo  , donde
, donde 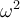 es simplemente el coeficiente positivo que multplica a la función
es simplemente el coeficiente positivo que multplica a la función 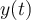 .
.