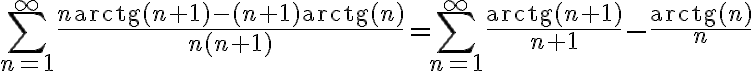Buenas!
La serie podes reescribirla separando los términos de la fracción que se están restando y cancelando parte del denominador:
Así nos queda la expresión de una telescópica, porque tenemos la resta entre un paso y el anterior, si desarrollamos la sumatoria se van a ir cancelando términos dos a dos y podemos llegar a una expresión "linda" para la reducida enésima.
Si ya probaste con esto y no salió decime y desarrollamos el problema un poco más :)
Saludos!
Florencia