Buenas, quisiera saber si está bien la forma de demostrar la corrección de mi algoritmo.
ALGORITMO:
1- Sea G un grafo, u un vértice del mismo, S un grafo vacío y flag un boolean inicializado en false.
2- TieneCiclo(u,u,S,flag);
3- TieneCiclo(u,v,S,flag){ //u vértice actual, v vértice padre.
4- Marque 'u' como explorado, y agregue 'u' a S
5- Para cada arista (u,w) incidente en 'u'
6- If 'w' no está explorada, entonces
7- invocar recursivamente TIeneCiclo(w,u,S,flag)
8- else if 'w'!='v' entonces flag=true
9- Endfor
10-}
Supongamos que flag==true, en tal caso, nuestro algoritmo nos afirma que G tiene un ciclo.
Observar que de la única forma que flag puede ser true es por la instrucción 8; en la cual entró al else y al if.
Si entró al if es porque encontró un vértice 'w' adyacente al vértice 'u', el cual ya estaba explorado y no era 'v', el vértice por el cual se llegó a 'u'.
Más gráficamente:
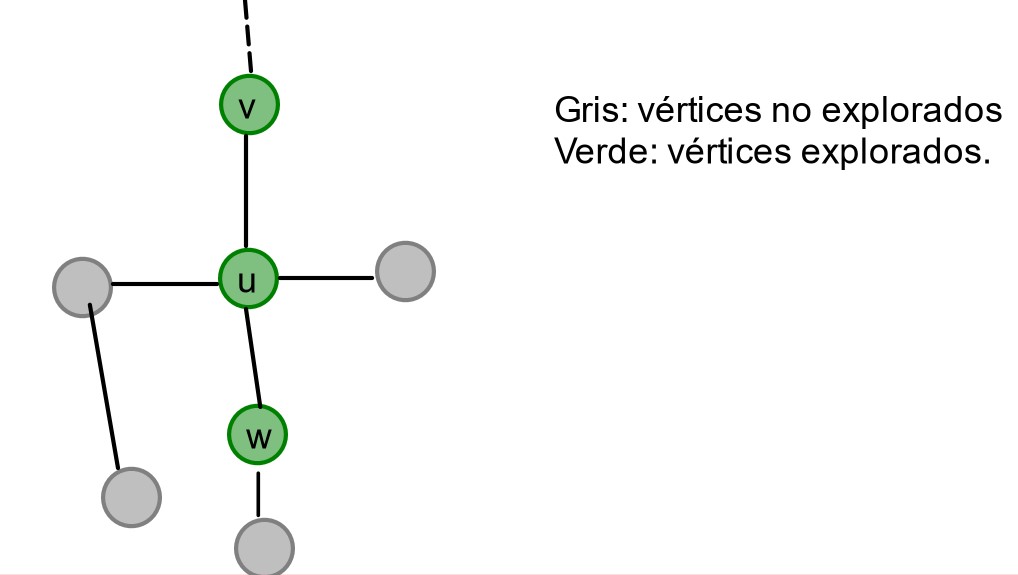
Si 'w' ya estaba explorado, entonces se tiene que haber ejecutado la instrucción 4 con w, viniendo de la invocación recursiva de TieneCiclo(w,p,S,flag) siendo 'p' un nodo adyacente a 'w'.
Más gráficamente:
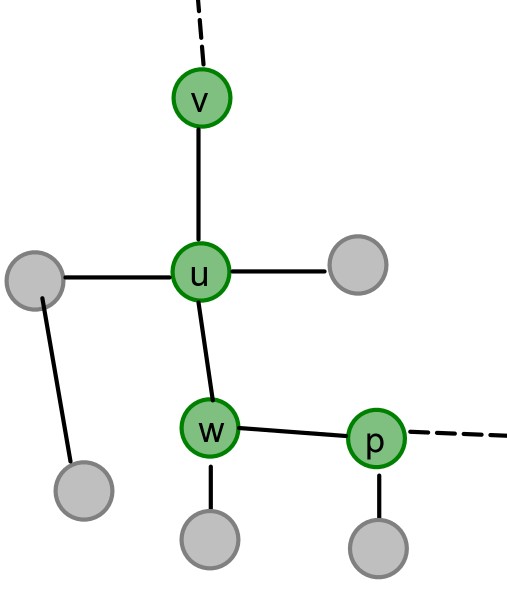
Llegados hasta aquí, hay dos opciones. Que 'p'=='v', en tal caso, se evidencia un ciclo.
O que 'p'!='v', en este caso, se repite el razonamiento anterior concluyendo que debe haber nodo ya explorado por el cual se llegó a 'p'.
Observar que puede ser que se repita el razonamiento hasta llegar al nodo de partida.
Falta la otra parte del si solo si.
Comentario: Quizás el algoritmo no esté del todo formal ya que, en parte, está escrito en pseudocódigo.