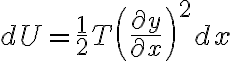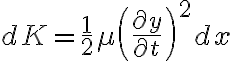Foro de Consultas Ejercicios y Teórico

Hola Pablo,

en primer lugar es conveniente tener en cuenta que en su forma infinitesimal las energías potencial y cinética pueden escribirse como

$dU=\frac{1}{2}T \left(\frac{\partial y}{\partial x}\right)^2 dx$ y $dK=\frac{1}{2}\mu \left(\frac{\partial y}{\partial t}\right)^2 dx$,

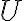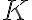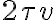respectivamente. Por lo tanto, para hallar $U$ y $K$ hay que integrar en la variable $x$. Para realizar esta integral es útil tener en cuenta que, debido a la información brindada en la letra, la base del pulso triangular mide $2\tau v$. Además, por tratarse de un pulso triangular se tiene

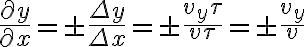$\frac{\partial y}{\partial x}=\pm \frac{\Delta y}{\Delta x}=\pm \frac{v_y \tau}{v \tau}=\pm \frac{v_y}{v}$, donde el signo está relacionado con el sentido de la velocidad vertical (hacia arriba o hacia abajo).

Saludos,

Nahuel