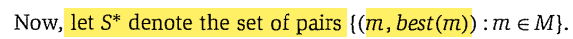Consultas 2022

Me cuesta un poco entender la pregunta.

 

la frase de "para toda persona se verifica que su mejor pareja válida coincide con su peor pareja válida" se refiere a que ninguna persona (ni cuando eligio M o cuando eligió W) terminó con su mejor opción.

Yo diría que al revés, si la mejor pareja válida es la peor pareja válida todos los individuos terminaron siempre con la mejor opción. ¿Puede ser que venga de ahí la confusión?

 

 

Un poco de contexto:

 

Dada una instancia del problema (conjuntos $M, W$ de tamaños $n$, con listas de preferencias concretas) pueden existir múltiples emparejamientos estables. En el ejercicio 1, parte b construyen un ejemplo de esto.

 

Lo que se prueba en el libro es que las ejecuciones de G-S siempre generan el mismo emparejamiento estable, y es "el mejor para los hombres" (para cada hombre, si miramos el conjunto de todas las mujeres que pueden aparecer en algún emparejamiento estable con él, G-S le da la que está más arriba en su lista de preferencias). Más aún, es también el "peor para todas las mujeres". (para cada mujer, si miramos el conjunto de todos los hombres que pueden aparecer en algún emparejamiento estable con ella, G-S le da el que está más abajo en su lista de preferencias).

 

En principio no está claro que el conjunto  $\{ (m, best(m)) | m \in M \}$ sea siquiera un emparejamiento, mucho menos estable, pero eso es lo que se prueba con esos enunciados del libro: eso es exactamente la salida de G-S. Así que de todos los emparejamientos estables posibles, hay uno que es absolutamente el mejor posible para cada hombre y a su vez el peor para cada mujer.

 

Ahora, si consideramos la versión alternativa del algoritmo donde proponen las mujeres, se da lo opuesto: el emparejamiento es el mejor posible para las mujeres y el peor posible para los hombres.

 

Ahora, si estos dos emparejamientos coinciden ¿qué se puede deducir?