Hola Tatiana, en efecto. Debes considerar lo que sucede en cero y en el infinito.
Para estudiar el comportamiento en el infinito, puedes notar que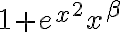 es equivalente a
es equivalente a 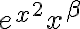 . Por lo tanto la integral impropia que debes considerar es
. Por lo tanto la integral impropia que debes considerar es 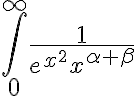 . Esta última es convergente en el infinito, pues estas comparando una exponencial con una función polinómica.
. Esta última es convergente en el infinito, pues estas comparando una exponencial con una función polinómica.
Para estudiar el comportamiento en el infinito, puedes notar que
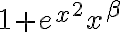 es equivalente a
es equivalente a 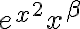 . Por lo tanto la integral impropia que debes considerar es
. Por lo tanto la integral impropia que debes considerar es 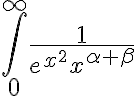 . Esta última es convergente en el infinito, pues estas comparando una exponencial con una función polinómica.
. Esta última es convergente en el infinito, pues estas comparando una exponencial con una función polinómica. Saludos
