Buenas, quisiera saber como resolver este ejercicio.
Se que de cero a uno la integral impropia converge, si alfa menor a uno. Pero se me esta complicando para ver la convergencia o divergencia de la integral desde uno a más infinito.
Buenas, quisiera saber como resolver este ejercicio.
Se que de cero a uno la integral impropia converge, si alfa menor a uno. Pero se me esta complicando para ver la convergencia o divergencia de la integral desde uno a más infinito.
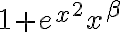 es equivalente a
es equivalente a 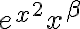 . Por lo tanto la integral impropia que debes considerar es
. Por lo tanto la integral impropia que debes considerar es 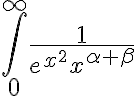 . Esta última es convergente en el infinito, pues estas comparando una exponencial con una función polinómica.
. Esta última es convergente en el infinito, pues estas comparando una exponencial con una función polinómica.