Buenas, tengo una consulta.
No entiendo el primer paso, cuando eleva raíz de x al cuadrado y cambia la integral de 1 a 4 a de 1 a 2 multiplicándola por dos, que propiedad uso?
muchas gracias
Buenas, tengo una consulta.
No entiendo el primer paso, cuando eleva raíz de x al cuadrado y cambia la integral de 1 a 4 a de 1 a 2 multiplicándola por dos, que propiedad uso?
muchas gracias
 es una primitiva de
es una primitiva de  , Barrow dice que
, Barrow dice que  . También, como
. También, como 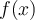 es una primitiva de
es una primitiva de  , Barrow dice que
, Barrow dice que  . Conclusión:
. Conclusión:  . (Observar cómo cambian los extremos de integración.)
. (Observar cómo cambian los extremos de integración.) y queremos hacer un cambio de variable con
y queremos hacer un cambio de variable con  . Para eso, debería aparecer el
. Para eso, debería aparecer el 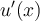 multiplicando (como en la fórmula de arriba). Como no está
multiplicando (como en la fórmula de arriba). Como no está  , lo que hace es "hacer que aparezca", multiplicando y dividiendo por él:
, lo que hace es "hacer que aparezca", multiplicando y dividiendo por él:
 . Para hacer el cambio de variable, falta decir quién es la
. Para hacer el cambio de variable, falta decir quién es la 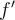 . Si llamamos
. Si llamamos  , nos queda
, nos queda  , y ya podemos usar la fórmula:
, y ya podemos usar la fórmula: 