No entiendo por que en la forma de orden inverso de integración se da que y está acotado inferiormente por 1, no entiendo de done sale ese 1 
Buenas, Alejandro.
Fijate que los extremos iniciales son:
1)
2)
Si querés ver los extremos de , fijate que el menor valor que toma es 1, y el mayor valor que toma es
, fijate que el menor valor que toma es 1, y el mayor valor que toma es  con
con 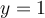 , pues tenemos que ver la forma de maximizar
, pues tenemos que ver la forma de maximizar  con
con  entre 1 y 2. Ahora, para los extremos de
entre 1 y 2. Ahora, para los extremos de  , fijate que por 1),
, fijate que por 1), 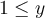 (acá está la cota que no entendías) y por 2), haciendo inversos de ambos lados,
(acá está la cota que no entendías) y por 2), haciendo inversos de ambos lados,  .
.
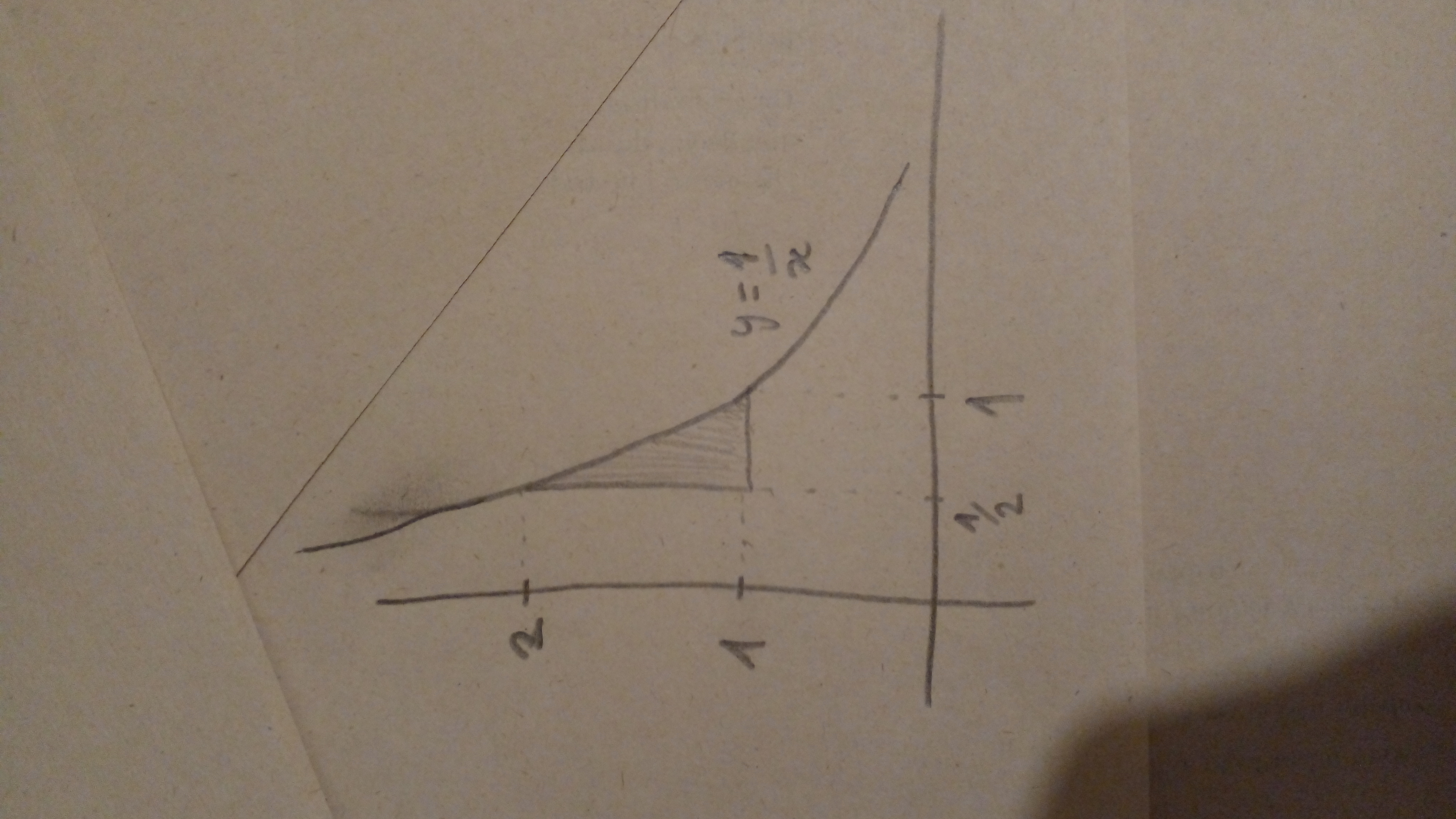
Capaz también este dibujito te ayuda a entenderlo mejor. Lo construí siguiendo las dos reglas iniciales.
Fijate que los extremos iniciales son:
1)

2)

Si querés ver los extremos de
 , fijate que el menor valor que toma es 1, y el mayor valor que toma es
, fijate que el menor valor que toma es 1, y el mayor valor que toma es  con
con 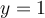 , pues tenemos que ver la forma de maximizar
, pues tenemos que ver la forma de maximizar  con
con  entre 1 y 2. Ahora, para los extremos de
entre 1 y 2. Ahora, para los extremos de  , fijate que por 1),
, fijate que por 1), 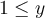 (acá está la cota que no entendías) y por 2), haciendo inversos de ambos lados,
(acá está la cota que no entendías) y por 2), haciendo inversos de ambos lados,  .
.Capaz también este dibujito te ayuda a entenderlo mejor. Lo construí siguiendo las dos reglas iniciales.
Saludos.