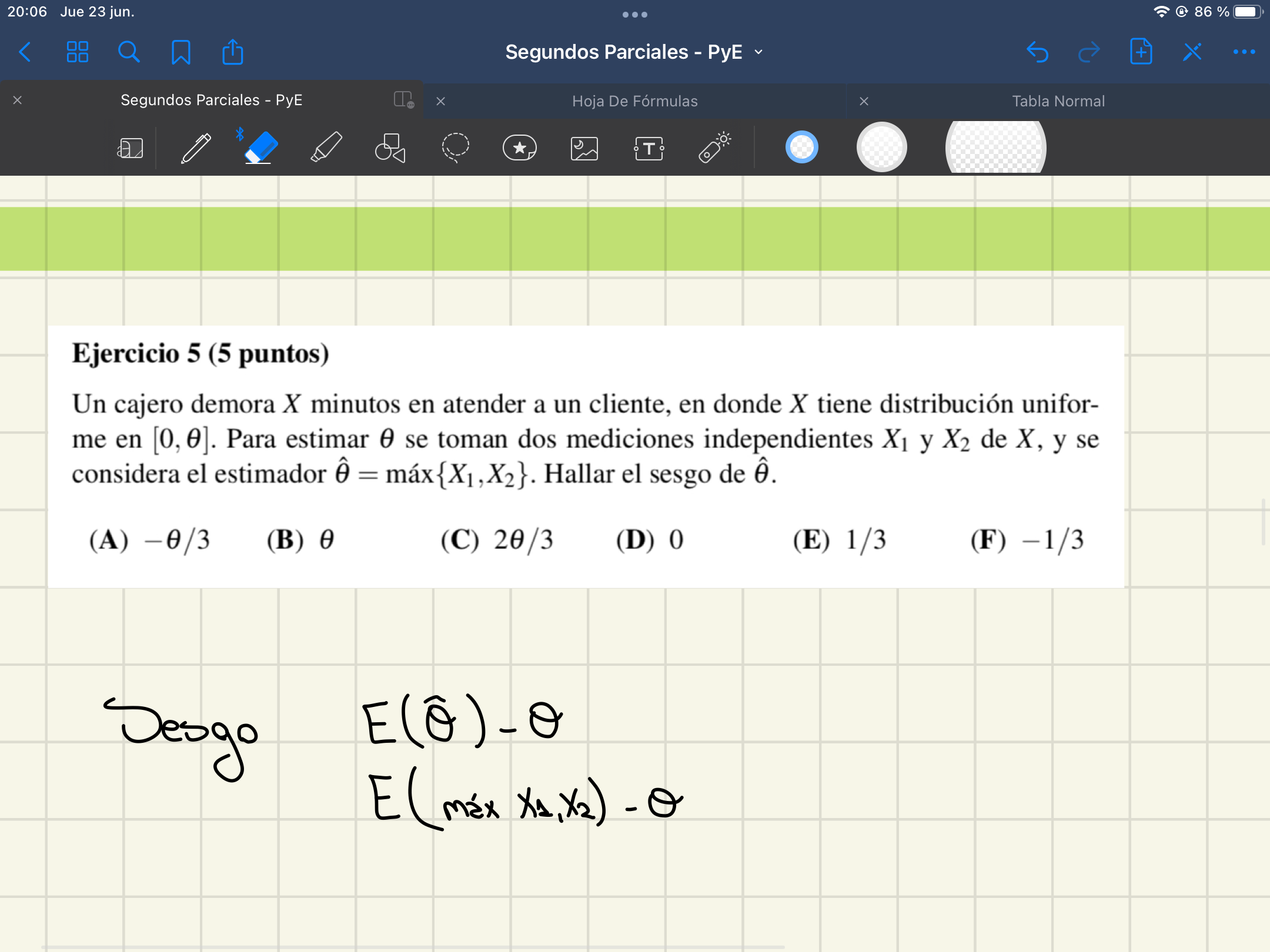
Hola, no entiendo este ejercicio y no entendí la solución, si alguien tiene el desarrollo o pueda explicarme agradezco. 

En respuesta a Romina Sosa Pereira Da Terra
Re: 2019 segundo semestre ejercicio 5
de Eduardo Canale -
Hola Romina, tu planteo es correcto, lo que te falta es calcular la esperanza del máximo de X1 y X2, para ello usas la fórmula de la esperanza: \( \mathbb{E} \max(X_1,X_2) = \int_{\mathbb{R}} t f_{ \max(X_1,X_2)}(t)dt \).
En la solución hallan la densidad \(f_{ \max(X_1,X_2)}(t)\) derivando la función de distribución \( F_{ \max(X_1,X_2)}(t) = P(\max(X_1,X_2) \leq t) = P(\hat \theta \leq t) \). Luego sigue la solución que hay en la web.
En la solución hallan la densidad \(f_{ \max(X_1,X_2)}(t)\) derivando la función de distribución \( F_{ \max(X_1,X_2)}(t) = P(\max(X_1,X_2) \leq t) = P(\hat \theta \leq t) \). Luego sigue la solución que hay en la web.
