
En respuesta a Agustín Cima Caballero
Re: Duda pendiente clase de consulta Marco
de Marco Antonio Perez -
Hola, Agustín.
Te sugiero que encuentres los valores de en la base canónica de
en la base canónica de 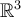 y extiendas por linealidad. Por ejemplo, para hallar
y extiendas por linealidad. Por ejemplo, para hallar  , sabes que se tiene que cumplir que
, sabes que se tiene que cumplir que  para todo
para todo  . Ten en cuenta que
. Ten en cuenta que  es un elemento de
es un elemento de 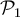 , por lo que
, por lo que  . El problema se reduce a hallar
. El problema se reduce a hallar  y
y  en
en 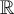 . Esto lo haces sustituyendo
. Esto lo haces sustituyendo 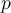 en la base canónica de
en la base canónica de 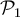 , es decir,
, es decir,  y
y  . Desarrollando estas igualdades, vas a poder determinar
. Desarrollando estas igualdades, vas a poder determinar  y
y  y obtener así
y obtener así  . Con ese mismo procedimiento, puedes hallar
. Con ese mismo procedimiento, puedes hallar  y
y  .
.
Saludos,
Marco
Te sugiero que encuentres los valores de
 en la base canónica de
en la base canónica de 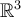 y extiendas por linealidad. Por ejemplo, para hallar
y extiendas por linealidad. Por ejemplo, para hallar  , sabes que se tiene que cumplir que
, sabes que se tiene que cumplir que  para todo
para todo  . Ten en cuenta que
. Ten en cuenta que  es un elemento de
es un elemento de 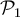 , por lo que
, por lo que  . El problema se reduce a hallar
. El problema se reduce a hallar  y
y  en
en 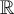 . Esto lo haces sustituyendo
. Esto lo haces sustituyendo 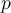 en la base canónica de
en la base canónica de 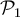 , es decir,
, es decir,  y
y  . Desarrollando estas igualdades, vas a poder determinar
. Desarrollando estas igualdades, vas a poder determinar  y
y  y obtener así
y obtener así  . Con ese mismo procedimiento, puedes hallar
. Con ese mismo procedimiento, puedes hallar  y
y  .
. Saludos,
Marco