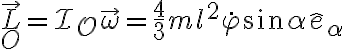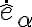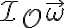Foro: parciales y exámenes

Hola, Juan Manuel. Excelente pregunta. Tu planteo tiene buen aspecto y no es tan sencillo detectar cuál es el problema. Veamos si podemos dilucidar el asunto.

Dado que ambos caminos parecen estar aplicando el mismo concepto, tenemos que buscar la razón por la cual no coinciden para tratar de entender el problema. Observamos que en ambos casos aparece el momento angular escrito como

$\vec L_O = \mathcal I _O \vec \omega = \frac 4 3 m l^2 \dot \varphi \sin \alpha \hat e_\alpha$

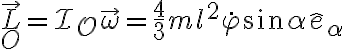
En el primer camino, al derivar la expresión anterior nos aparece un término debido a la derivada 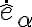$\dot {\hat e}_\alpha$ que no aparece en el segundo camino... ¡Ajá! La forma en que estamos derivando el momento angular en el segundo camino puede estar mal.

En efecto, al escribir el momento angular 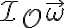$\mathcal I_O \vec \omega$, implícitamente estamos utilizando un referencial relativo, que es solidario al rígido. Pero la derivada la queremos calcular en el referencial fijo (el "absoluto").

Entonces tenemos que poner

$\dfrac {d (\mathcal I_O \vec \omega)}{dt} = \dfrac {d' (\mathcal I_O \vec \omega)}{dt} + \vec \omega \times (\mathcal I_O \vec \omega)$

(utilizando la relación entre la derivada absoluta y la derivada relativa; ver página 102 del archivo de Apuntes del Curso).

Esto revela que lo que calculaste en el segundo camino es en realidad solamente el primer término: es la derivada relativa del momento angular. Al calcular la derivada completa, ambas expresiones van a coincidir, como corresponde.

¿Se entendió? ¿Te animas a verificar si usando la derivada corregida llegas a lo mismo? Contanos si consigues resolver el problema o si quedan más dudas.

Saludos,
NC