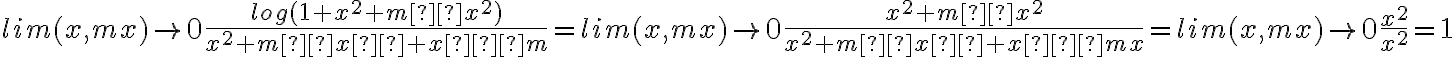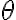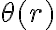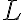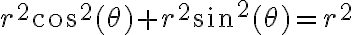CDIVV - 1S: Ejercicio 8f

Buenas, al hacer este ejercicio use algunas cosas que, si bien llego al resultado, no se si son del todo correctas.

Primero uso una especie de equivalentes en varias variables que no se si esta bien. Luego una vez que tengo la equivalencia trabajo con polares para tener una sola variable $r$ y poder aplicar Taylor de toda la vida.

Dejo del desarrollo. O sea la pregunta en si es si esta bien resulto o hay algo que no es del todo correcto en cuanto a planteo, por mas que el resultado es el esperado.

Saludos.

Re: Ejercicio 8f

de Diego Wandarley Garrido Rosado - jueves, 2 de junio de 2022, 21:14

Buenas, yo tengo la misma duda. Usando la equivalencia para el logaritmo y luego polares llego a 1/1+r2(cos3Θ)(senΘ) cuyo limite claramente es 1 si r tiende a 0.
De todas formas con este resultado no estoy seguro si puedo asegurar el limite en 1 para f(x,y) ya que el reciproco de el ejercicio 4)b) no se cumple siempre.

Re: Ejercicio 8f

de Alejandro Sena Peraza - sábado, 4 de junio de 2022, 16:41

Me sumo a sus dudas, no se si es legal usar los equivalentes usuales en limites con varias variables(pasa lo mismo en e).
En este caso me pude saltear ese detalle mirando que pasa si y=mx.
Queda un limite de 1 variable x->0. Ahí si uso el equivalente y luego infinitesimos para llegar al resultado con seguridad.

$lim (x,mx) \rightarrow0 \frac{log(1+x^2+m²x^2)}{x^2+m²x²+x⁴m} = lim (x,mx) \rightarrow0 \frac{x^2+m²x^2}{x^2+m²x²+x⁴mx} = lim (x,mx) \rightarrow0 \frac{x^2}{x^2} = 1$

Re: Ejercicio 8f

de Geronimo De Leon Ramirez - lunes, 6 de junio de 2022, 20:09

Buenas a todos.

Nicolás:
Siempre que pruebes que el límite del cociente entre las dos cosas que querés intercambiar sea 1, podés cambiarlos, como hiciste en este caso. Tenés que tener cuidado ya que estás usando en algún lado que el límite del producto es el producto de los límites, y esto es cierto siempre y cuando ambos límites existan, pero lo usaste bien. Todo el proceso está correcto. Podés intentar probar que las reglas de equivalentes de una variable sirven también en dos variables pasando a polares, ya que el límite pasa a ser sólo con r tendiendo a infinito.

Diego:
El recíproco del 4)b) no se cumple porque el

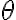
$\theta$ está fijo, por lo que el límite que hace es acercarse por rectas (o sea, un ángulo fijo), pero si no ponés la condición de que

$\theta$ esté fijo (por ejemplo, en vez de

$\theta$ le llamás

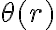
$\theta(r)$ ) y probás que el límite existe y es

$L$ , entonces pasás a usar la parte a) en donde sí valía el recíproco, y fijate que en este caso no necesitamos usar que

$\theta$ estaba fijo en todo momento ya que la ecuación

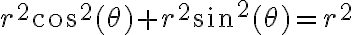
$r^2cos^2(\theta)+r^2sin^2(\theta)=r^2$ valía de igual forma.

Alejandro:
Igual que a Nicolás, es legal siempre que pruebes que el límite del cociente de las cosas que querés intercambiar sea 1, entonces, cambiás un límite por el otro. La parte e) que decís está bien, podés usar las equivalencias con menos miedo porque estás en una variable, pero eso no alcanza para ver que el límite existe ya que acercarse por rectas no es suficiente, aunque como el ejercicio dice "Calcular", podés asumir que existen y calcularlos de la forma que te quede más práctico.

Saludos.