Buenas Noches. tengo una duda sobre el ej 13.1. Entiendo como resolver el ejercicio pero no me queda claro por que debe ser una base ortonormal y no una base cualquiera del subespacio S. Gracias
Hola, Matias:
Te recomiendo que repases la definición de proyección ortogonal. Más específicamente, cómo se construye el vector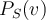
.
Básicamente, el problema es que si construyes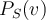 usando una base de 
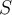que no es ortonormal, no tienes garantía de que el vector 
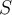sea ortogonal a (que es justamente lo que se busca cuando se construye la proyección ortogonal). Puedes probar con un ejemplo concreto para darte cuenta, por ejemplo, tomando 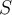en plano 
contenido en 
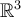, con base 
(que no es ortogonal), y proyectar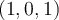 
.
Saludos,
Marco
Te recomiendo que repases la definición de proyección ortogonal. Más específicamente, cómo se construye el vector
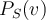.Básicamente, el problema es que si construyes
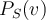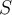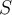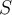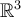usando una base de que no es ortonormal, no tienes garantía de que el vector sea ortogonal a (que es justamente lo que se busca cuando se construye la proyección ortogonal). Puedes probar con un ejemplo concreto para darte cuenta, por ejemplo, tomando en plano contenido en , con base (que no es ortogonal), y proyectar 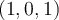. Saludos,
Marco