Lo primero a tener en cuenta es que para el modelo exponencial del diodo:
Para fijar ideas, si calculamos el voltaje
 para que
para que  , obtenemos:
, obtenemos:
O sea que podemos usar un modelo simplificado de diodo Zener de 2 zonas para
 :
:Si usas esas ecuaciones de zona y esas verificaciones, podes comprobar que para los casos del ejercicio 5.b., si supones que ambos diodos D1 y D2 están en zona inversa, podes verificar que  y por lo tanto concluir que la suposición era correcta.
y por lo tanto concluir que la suposición era correcta.
Otra forma de verlo es gráficamente dibujando la característica del diodo Zener.
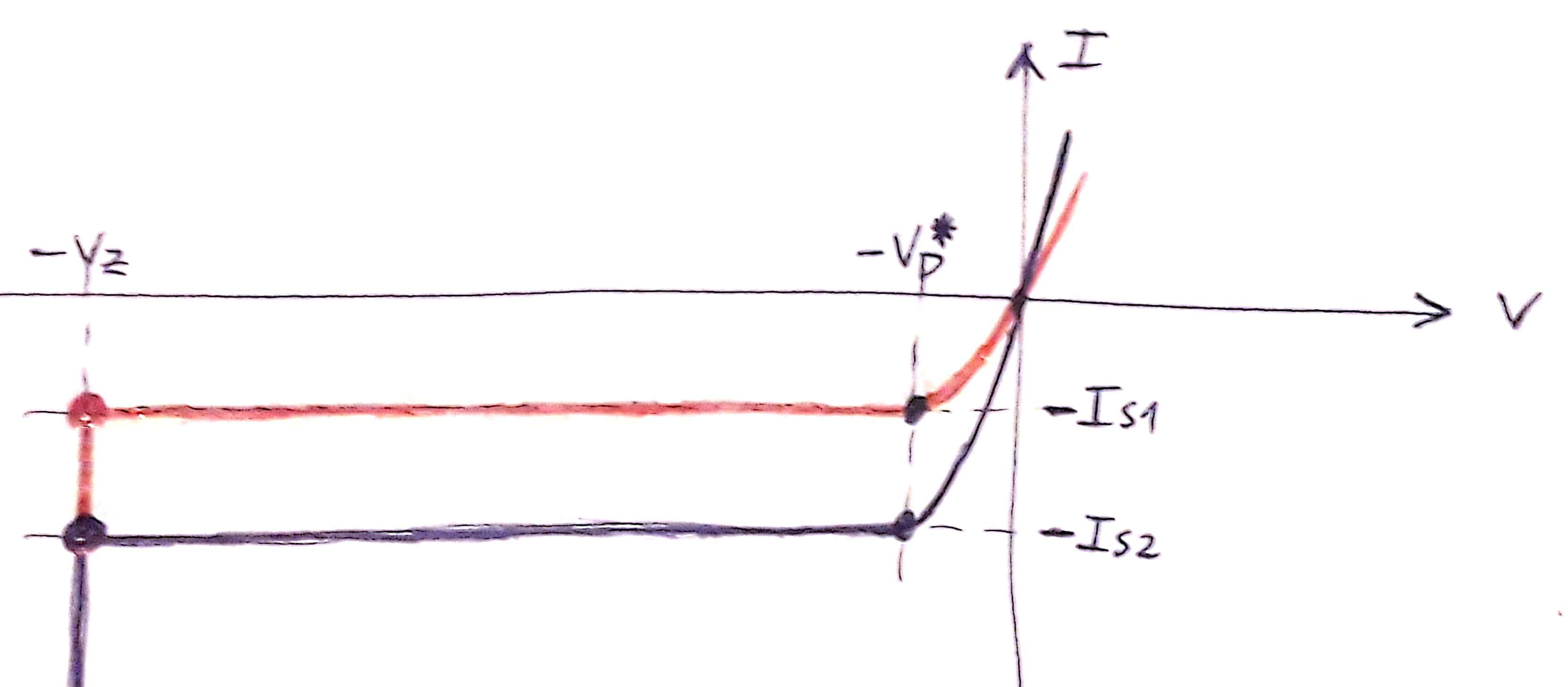
En el caso de la parte 5.a (diodos D1 y D2 en serie), lo que hace que los voltajes se repartan de forma muy desigual es que para un rango de  , los voltajes
, los voltajes  y
y  son muy distintos. En particular, para corrientes
son muy distintos. En particular, para corrientes  entre
entre  y
y  , los voltajes difieren aproximadamente
, los voltajes difieren aproximadamente  :
:
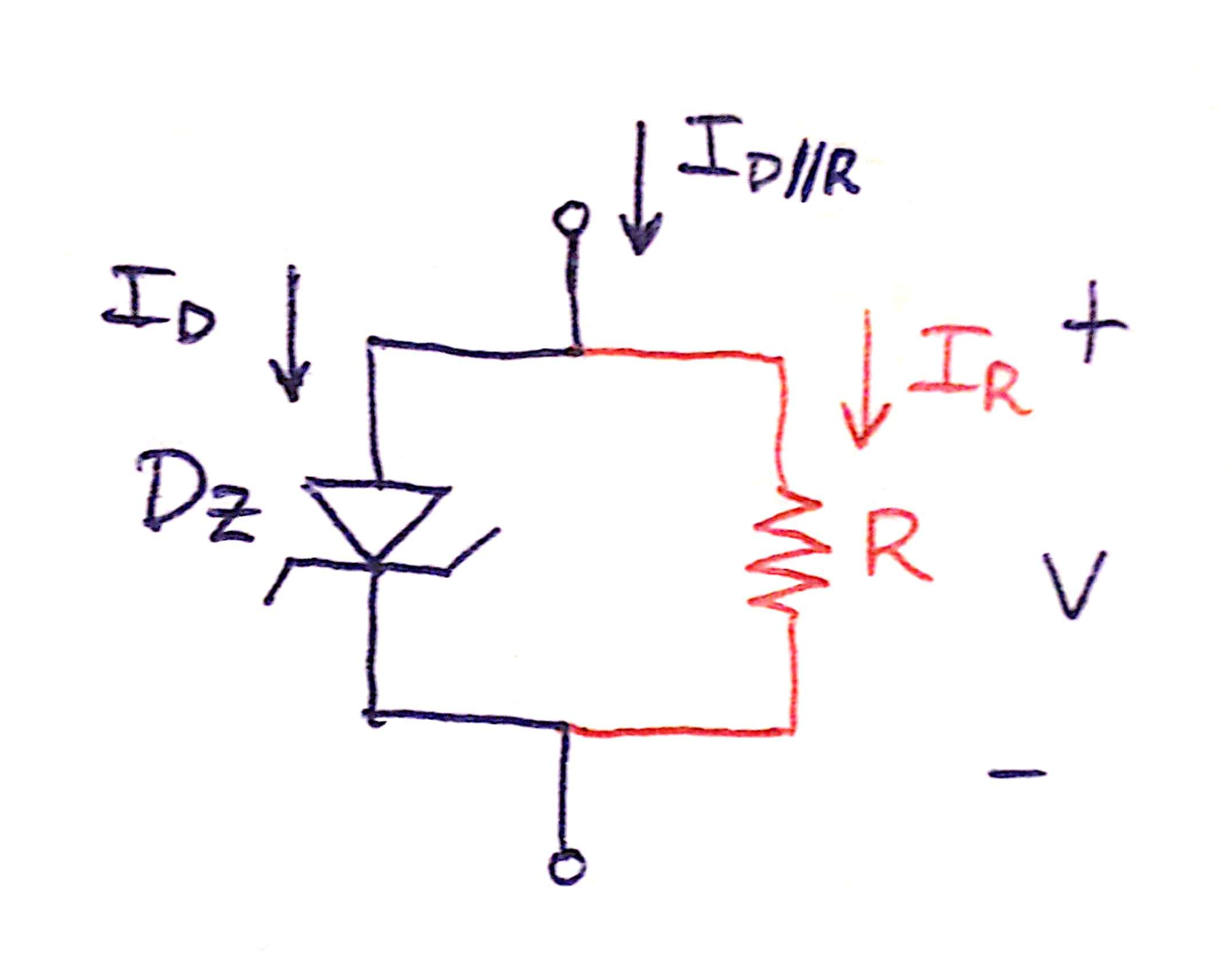
En el caso de la parte 5.b, se agrega a cada diodo Zener una resistencia R en paralelo:
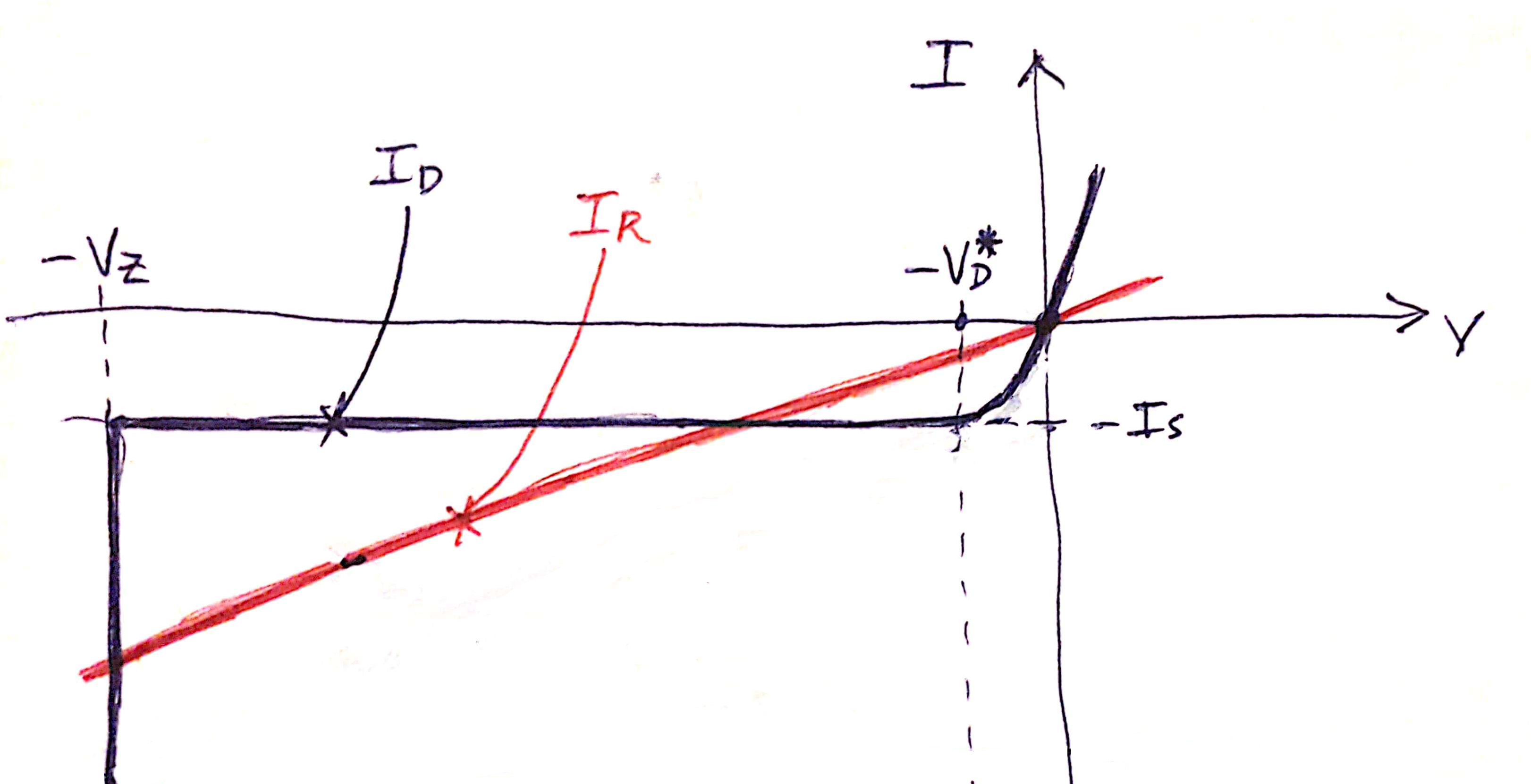
La característica de un diodo Zener (en azul) y una resistencia R (en rojo) es como sigue:
Como están en paralelo, se puede pensar la característica de (diodo Zener // resistencia R) como si fuera un único componente, y para obtenerla simplemente hay que sumar las dos anteriores, ya que como están en paralelo, para un mismo voltaje, la corriente será la suma:  .
.
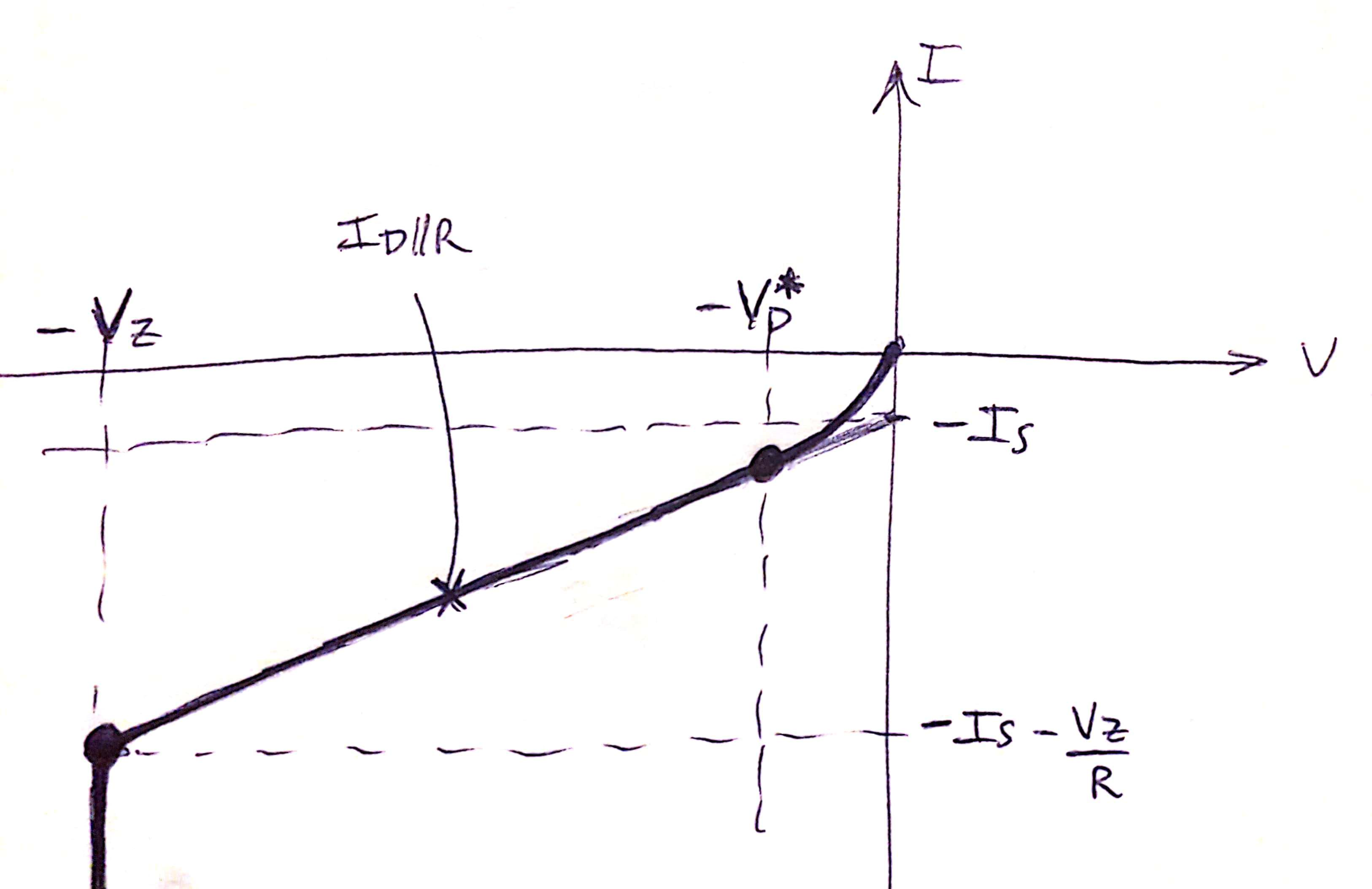
Con la nueva característica de (diodo Zener // resistencia R), si ponemos dos en serie, uno con  y el otro con
y el otro con  , la diferencia de voltaje entre las dos características pasará a ser a lo sumo
, la diferencia de voltaje entre las dos características pasará a ser a lo sumo  en la zona en la que ambos diodos están en zona inversa. El desequilibrio de voltaje se redujo muchísimo. Como hay 10 V de diferencia a lo sumo entre
en la zona en la que ambos diodos están en zona inversa. El desequilibrio de voltaje se redujo muchísimo. Como hay 10 V de diferencia a lo sumo entre  y
y  , si se aplica
, si se aplica  o
o  , es imposible que alguno de los diodos D1 o D2 esté en zona Zener (porque aplicando mallas
, es imposible que alguno de los diodos D1 o D2 esté en zona Zener (porque aplicando mallas  ). Por lo tanto, ambos están en zona inversa.
). Por lo tanto, ambos están en zona inversa.
Saludos!






