Hola, Santiago:
Aunque la base sea la canónica, se trata de una base en el espacio de polinomios de grado menor o igual que dos. Esto último es muy importante, ya que los vectores propios serán entonces polinomios, mientras que es un elemento de
es un elemento de 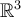 .
.
En general, si tienes un espacio vectorial de dimensión
de dimensión  , la función
, la función  define un isomorfismo de
define un isomorfismo de  a
a 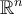 . Cuando
. Cuando  y
y 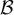 es la base canónica de
es la base canónica de 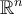 , entonces este isomorfismo es de hecho una igualdad. Sin embargo, esto último no era lo que ocurría en el parcial, pues
, entonces este isomorfismo es de hecho una igualdad. Sin embargo, esto último no era lo que ocurría en el parcial, pues  y
y 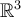 son distintos (aunque isomorfos).
son distintos (aunque isomorfos).
Saludos,
Marco
Aunque la base sea la canónica, se trata de una base en el espacio de polinomios de grado menor o igual que dos. Esto último es muy importante, ya que los vectores propios serán entonces polinomios, mientras que
 es un elemento de
es un elemento de 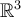 .
. En general, si tienes un espacio vectorial
 de dimensión
de dimensión  , la función
, la función  define un isomorfismo de
define un isomorfismo de  a
a 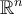 . Cuando
. Cuando  y
y 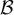 es la base canónica de
es la base canónica de 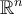 , entonces este isomorfismo es de hecho una igualdad. Sin embargo, esto último no era lo que ocurría en el parcial, pues
, entonces este isomorfismo es de hecho una igualdad. Sin embargo, esto último no era lo que ocurría en el parcial, pues  y
y 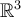 son distintos (aunque isomorfos).
son distintos (aunque isomorfos). Saludos,
Marco