Buenas noches, quería consultar a qué funciones se está refiriendo el ejercicio, porque a mi entender sólo se dan imágenes de puntos de una misma función f. Gracias.
En respuesta a Silvina Maria Blanco Celaya
Re: Parcial 2020 segundo semestre. Ej 3
Lo que dice el ejercicio es: "se consideran las funciones continuas ![f:[0,2]\to(0,5) f:[0,2]\to(0,5)](https://eva.fing.edu.uy/filter/tex/pix.php/7d54ad41cd7f11eb300d6ced803b00da.png) tales que
tales que 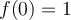 ,
, 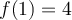 y
y 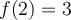 ..."
..."
O sea, imagínate todas las funciones posibles que cumplan esas condiciones... hay muchas. Básicamente, dibujate un par de ejes en donde se vea el intervalo![[0,2] [0,2]](https://eva.fing.edu.uy/filter/tex/pix.php/70fd3f388413505934da60b43afc4088.png) (eje
(eje  ) y el intervalo
) y el intervalo 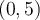 (eje
(eje  ), y dibujá funciones que pasen por los puntos
), y dibujá funciones que pasen por los puntos 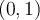 ,
, 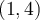 y
y 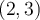 sin levantar el lápiz. Lo de "no levantar el lápiz" viene de la condición "
sin levantar el lápiz. Lo de "no levantar el lápiz" viene de la condición " es continua (en todo punto del
es continua (en todo punto del ![[0,2] [0,2]](https://eva.fing.edu.uy/filter/tex/pix.php/70fd3f388413505934da60b43afc4088.png) )". Además, se tiene que cumplir que todas las imágenes de
)". Además, se tiene que cumplir que todas las imágenes de  caigan entre 0 y 5.
caigan entre 0 y 5.
Ta, si sos creativa, vas a poder dibujar funciones que te ayuden a responder el múltiple opción.
![f:[0,2]\to(0,5) f:[0,2]\to(0,5)](https://eva.fing.edu.uy/filter/tex/pix.php/7d54ad41cd7f11eb300d6ced803b00da.png) tales que
tales que 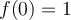 ,
, 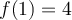 y
y 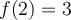 ..."
..."O sea, imagínate todas las funciones posibles que cumplan esas condiciones... hay muchas. Básicamente, dibujate un par de ejes en donde se vea el intervalo
![[0,2] [0,2]](https://eva.fing.edu.uy/filter/tex/pix.php/70fd3f388413505934da60b43afc4088.png) (eje
(eje  ) y el intervalo
) y el intervalo 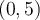 (eje
(eje  ), y dibujá funciones que pasen por los puntos
), y dibujá funciones que pasen por los puntos 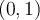 ,
, 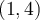 y
y 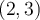 sin levantar el lápiz. Lo de "no levantar el lápiz" viene de la condición "
sin levantar el lápiz. Lo de "no levantar el lápiz" viene de la condición " es continua (en todo punto del
es continua (en todo punto del ![[0,2] [0,2]](https://eva.fing.edu.uy/filter/tex/pix.php/70fd3f388413505934da60b43afc4088.png) )". Además, se tiene que cumplir que todas las imágenes de
)". Además, se tiene que cumplir que todas las imágenes de  caigan entre 0 y 5.
caigan entre 0 y 5. Ta, si sos creativa, vas a poder dibujar funciones que te ayuden a responder el múltiple opción.
En respuesta a Sofia Llavayol Alvariño
Re: Parcial 2020 segundo semestre. Ej 3
Sofía, me queda la duda de por qué esta función no es sobreyectiva. Entiendo por qué no es inyectiva, pero no lo primero. Agradecería pudieras echar luz sobre el asunto.
En respuesta a Lucas Elías Ricardi Almeida
Re: Parcial 2020 segundo semestre. Ej 3
Lucas, fíjate que el codominio es el intervalo 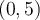 **abierto**. Entonces, cuando querés hacer una función continua que sea sobreyectiva en
**abierto**. Entonces, cuando querés hacer una función continua que sea sobreyectiva en 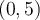 , necesariamente vas a tener un punto cuya imagen sea 5. Pero eso no está permitido; tus funciones tienen que cumplir
, necesariamente vas a tener un punto cuya imagen sea 5. Pero eso no está permitido; tus funciones tienen que cumplir  . ¿se entiende?
. ¿se entiende?
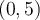 **abierto**. Entonces, cuando querés hacer una función continua que sea sobreyectiva en
**abierto**. Entonces, cuando querés hacer una función continua que sea sobreyectiva en 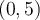 , necesariamente vas a tener un punto cuya imagen sea 5. Pero eso no está permitido; tus funciones tienen que cumplir
, necesariamente vas a tener un punto cuya imagen sea 5. Pero eso no está permitido; tus funciones tienen que cumplir  . ¿se entiende?
. ¿se entiende?Creo que no llegaron a esto en el teórico, pero la idea es que hay un teorema (Weierstrass) que de dice que la imagen de un intervalo cerrado por una función continua es un intervalo cerrado. En este caso, lo que estoy diciendo es que siempre va a pasar que ![f\big([0,2]\big)=[a,b] f\big([0,2]\big)=[a,b]](https://eva.fing.edu.uy/filter/tex/pix.php/f68755a375e8376c6ddb3fbf27988e9d.png) , para algunos valores
, para algunos valores  y
y  . Entonces no puede ser
. Entonces no puede ser 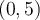 la imagen.
la imagen.
![f\big([0,2]\big)=[a,b] f\big([0,2]\big)=[a,b]](https://eva.fing.edu.uy/filter/tex/pix.php/f68755a375e8376c6ddb3fbf27988e9d.png) , para algunos valores
, para algunos valores  y
y  . Entonces no puede ser
. Entonces no puede ser 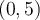 la imagen.
la imagen.
En respuesta a Sofia Llavayol Alvariño