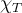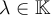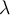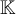Buenas noches.
Tengo una duda respecto a la afirmación 3 del ejercicio de verdadero y falso del primer parcial. La misma expresa: "Si T tiene tres valores propios distintos dos a dos, entonces T es diagonalizable".
Mi consulta es por qué dicha afirmación es verdadera si en ningún momento del enunciado se afirma que los tres valores propios pertenecen al cuerpo en el que se está trabajando (en este caso, los polinomios de grado menor o igual a dos). A mi entender, para que T sea diagonalizable, los valores propios deben ser distintos dos a dos y, además, deben pertenecer al cuerpo.
Aguardo su respuesta. Muchas gracias.