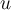CDIVV - 1S: Ej 5 primer parcial 2020 matutino

Buenas, vi la solución a este ejercicio y no entiendo cómo resuelve el límite para determinar que esas funciones son equivalentes cuando tienden a 0. También, hay algún tip para saber que función tomar como equivalente?

Re: Ej 5 primer parcial 2020 matutino

de Geronimo De Leon Ramirez - domingo, 1 de mayo de 2022, 21:48

Buenas.

Cuando

$x$ tiende a cero,

$sin(x)\sim x$ y

$e^x-1\sim x$ . Te queda entonces que:

$\frac{x^\alpha x^\beta}{sin(x)^\alpha(e^x-1)^\beta cos(x)^\gamma} \sim \frac{1}{cos(x)^\gamma}\sim 1$ . La clave está en las primeras equivalencias que escribí.

Sobre lo que pedís del tip, casi siempre es útil utilizar alguna de las siguientes equivalencias:

$sin(u)\sim log(1+u)\sim e^u-1\sim u$ cuando

$u$ tiende a cero.