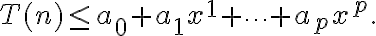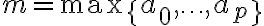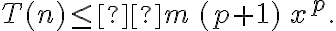¡Buenas!,
Estoy teniendo un poco de de dificultad para encontrar los c y n0 para las funciones de orden de crecimiento.
En el caso del algoritmo 3, sean: C1 : asignaciones, C2: comparaciones, C3 : incrementos, entonces la función de tiempo de ejecución me queda de la siguiente manera:
Luego, para hallar el c y n0, se me ocurren algunas formas (como definirme un h = max{C1, C2, C3} y de ahí usar n0 = 1 por ejemplo, o también completar las potencias del polinomio resultante de desarrollar T(n) por n^3 y así despejar c en función de C1, C2 y C3) pero no veo como demostrar de forma limpia que para todos los n >= n0 se va cumplir, más que en algún caso evidente como el algoritmo 1.
Desde ya muchas gracias,
Marco.