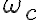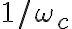Buenas, quisiera consultar sobre la parte d del ejercicio 8. No comprendo bien como fundamentar que al aumentar 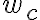 la respuesta al impulso se concentra más o menos al rededor del origen.
la respuesta al impulso se concentra más o menos al rededor del origen.
Llegué a que 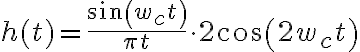 . Entiendo que al aumentar la frecuencia
. Entiendo que al aumentar la frecuencia 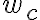 el
el 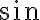 y
y  oscilan mas rápido, teniendo en cuenta que al rededor de 0 la amplitud va a ser grande, ya que
oscilan mas rápido, teniendo en cuenta que al rededor de 0 la amplitud va a ser grande, ya que 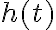 esta dividida por
esta dividida por 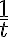 va a tender a achicarse su amplitud para tiempos grandes.
va a tender a achicarse su amplitud para tiempos grandes.
No entiendo si esa es la explicación o no.
Gracias, Rodrigo