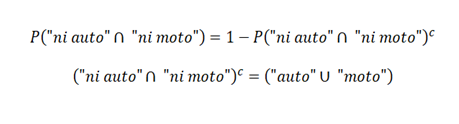Buenas tardes,
Estoy intentando hacer el ejercicio mencionado, pero no estoy llegando a la solución.

El razonamiento que estoy siguiendo es el siguiente:
Dibujo un árbol para seguir el experimento como este:

Donde asumo que el tener ambos vehículos se puede determinar por la probabilidad de tener auto por la probabilidad de tener moto. (quizás aquí está el error)
Tomando V como "tener ambos vehículos" y A,B Y C como "pertenece al país A", "pertenece al país B",... Llego a que:
P(V|A)=3/200 , P(V|B)=7/120 , P(V|C)=7/50
Entonces lo que debo hallar se podría tomar como P(B|V) es decir la probabilidad de pertenecer a B dado que se tiene auto y moto.
Tomando Bayes, puedo determinar esa probabilidad como:
P(B|V) = ( P(V|B) P(B) ) / ( P(V|A) P(A) + P(V|B) P(B) + P(V|C) P(C) )
Llegando a ( 7/120 * 1/3 ) / ( 3/200*1/6 + 7/360 + 7/50*1/2 ) = (7/360) / (331/3600)
Lo cual no se corresponde con la respuesta correcta.
Agradezco cualquier ayuda.